АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Інтегральна теорема Лапласа

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Внешние эффекты (экстерналии). Теорема Коуза.
  3. Внешние эффекты, их виды и последствия. Теорема Коуза
  4. Вопрос 1 теорема сложения вероятностей
  5. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  6. Вопрос. Теорема Котельникова (Найквиста)
  7. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  8. Гранична теорема Пуассона
  9. Дискретизація сигналу – теорема відліків (Котельникова)
  10. Друга теорема економіки добробуту та її значення
  11. Друга теорема розвинення
  12. Закон Био-Савара-Лапласа

Якщо число незалежних випробувань досить велике, а ймовірність появи події в кожному випробуванні не мала, то ймовірність появи події в інтервалі від до разів визначається наближеною формулою

, , .

Функція – непарна. Значення функції знаходять із таблиці (додаток 2). При .

 

Ймовірність відхилення відносної частоти від ймовірності. Нехай проводять незалежних випробувань, у кожному з яких ймовірність появи події постійна. Ймовірність того, що в випробуваннях відносна частота появи події відхилиться від ймовірності не більш, ніж на , визначається наближеною формулою

.

Найімовірніше число появ події в серії незалежних випробувань. Числопояв події в незалежних випробуваннях називається найімовірнішим, якщо його ймовірність є найбільшою

.

Якщо – ціле число, то ,

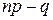§ – дробове число, то існує єдине , що дорівнює цілій частині числа ,

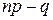§ – ціле число, то існує два найімовірніших числа, які дорівнюють відповідно лівій і правій частині нерівності.

 

 

Приклад 11. Ймовірність улучення в мішень при одному пострілі дорівнює 0,4. Знайти ймовірність 3-х улучень при 5-ти пострілах.

Розв’язання. За формулою Бернуллі визначимо ймовірність 3-х улучень при 5-ти пострілах .

 

Приклад 12. Підручник виданий тиражем 100 000 екземплярів. Ймовірність того, що підручник зброшурований неправильно, дорівнює 0,0001. Знайти ймовірність того, що тираж містить рівно 5 бракованих книг.

Розв’язання. За умовою . Використовуємо формулу Пуассона. ,

.

Приклад 13. 75% усієї продукції відповідає вимогам вищого сорту. Знайти ймовірність того, що в партії з 150 виробів: а) 100 виробів виявиться вищого сорту; б) не менш 110 виробів виявляться вищого сорту.

Розв’язання.

а) . Використаємо локальну теорему Лапласа.

Подія – поява виробу вищого сорту.

.

Із таблиці (додаток 1) знаходимо: , тоді

.

б) . Використаємо інтегральну теорему Лапласа

, ,

.

Отже

.

 

Приклад 14. Ймовірність появи події в кожному з 625 незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що відносна частота відхилитися від 0,8 не більш, ніж на 0,04.

Розв’язання.

.

.

 

Приклад 15. Ймовірність того, що деталь стандартна, дорівнює 0,9. Скільки необхідно перевірити деталей, щоб з ймовірністю 0,9544 можна було стверджувати, що частість відхилиться від ймовірності не більш, ніж на 0,02.

Розв’язання. .

, ,

із таблиці , , , .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)