 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Елементи комбінаторики. У розділі “Комбінаторний аналіз” вивчаються поняття, що дозволяють визначити без прямого перерахування різні можливі комбінації скінченного числа елементів
У розділі “Комбінаторний аналіз” вивчаються поняття, що дозволяють визначити без прямого перерахування різні можливі комбінації скінченного числа елементів деякої множини.
Принцип множення:
Нехай потрібно послідовно виконати  дій. Якщо першу дію можна виконати
дій. Якщо першу дію можна виконати 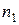 різними способами, другу –
різними способами, другу –  різними способами і так до
різними способами і так до  -ої дії, яку можна виконати
-ої дії, яку можна виконати  різними способами, то всі
різними способами, то всі  дій можна виконати
дій можна виконати  різними способами.
різними способами. 
Принцип додавання:
Якщо дві дії взаємно виключають одна одну, причому одну з них можна виконати  різними способами, а другу –
різними способами, а другу –  різними способами, то яку-небудь одну з них можна виконати
різними способами, то яку-небудь одну з них можна виконати  різними способами.
різними способами.
Перестановкою з  елементів називають упорядковане розташування цих елементів у певній лінійній послідовності.
елементів називають упорядковане розташування цих елементів у певній лінійній послідовності.
Різні перестановки з  елементів відрізняються порядком їх розташування. Число перестановок з
елементів відрізняються порядком їх розташування. Число перестановок з  елементів:
елементів:

Наприклад, з трьох елементів  можна скласти
можна скласти  перестановок:
перестановок:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Розміщенням з  елементів по
елементів по  елементів називається довільна упорядкована
елементів називається довільна упорядкована  -елементна підмножина
-елементна підмножина  -елементної множини.
-елементної множини.
Різні розміщення з  елементів по
елементів по  відрізняються одне від одного набором елементів або порядком їх розташування. Число розміщень з
відрізняються одне від одного набором елементів або порядком їх розташування. Число розміщень з  елементів по
елементів по  елементів знаходять таким чином:
елементів знаходять таким чином:

Наприклад, з трьох елементів  сформуємо групи по 2 елемента, їх кількість визначимо так:
сформуємо групи по 2 елемента, їх кількість визначимо так:  . Самі групи будуть такими:
. Самі групи будуть такими:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Сполученням з  елементів по
елементів по  називається довільна неупорядкована
називається довільна неупорядкована
 -елементна підмножина
-елементна підмножина  -елементної множини.
-елементної множини.
Різні сполучення з  елементів по
елементів по  відрізняються одне від одного набором елементів. Число сполучень з
відрізняються одне від одного набором елементів. Число сполучень з  елементів по
елементів по  елементів знаходиться так:
елементів знаходиться так:

Визначимо кількість груп по 2 елемента. З трьох елементів  :
:  . Отримаємо такі групи:
. Отримаємо такі групи:  ,
,  ,
,  .
.
Комбінації  і
і  являють собою одне сполучення.
являють собою одне сполучення.
Зауваження:  і т.д.
і т.д.
| Приклад. | Скільки існує різних тризначних чисел? |
Розв’язання.
Кожну цифру числа можна вибрати певною кількістю способів: першу – дев’ятьма (всі цифри підходять, крім нуля, інакше це буде не тризначне число), другу – десятьма і третю – десятьма способами. За принципом множення:  .
.
| Приклад. | Скількома способами можуть розподілитися призові місця на чемпіонаті з футболу, у якому беруть участь 12 команд? |
Розв’язання.
За принципом множення на перше місце можуть претендувати 12 команд, на друге – 11 (одна команда зайняла перше місце), на третє – 10. Отже, загальне число способів  .
.
За допомогою числа розміщень:
 .
.
| Приклад. | Скількома способами можна заповнити лотерейний квиток 5 з 36? |
Розв’язання.
Оскільки при заповненні квитка не важливий порядок вибору чисел, то кількість способів обчислюють за формулою числа сполучень:
 .
.
Поиск по сайту: