 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формула Бейєса. Якщо подія уже відбулася, то переоцінити ймовірність кожної гіпотези можна за формулою Бейєса
Якщо подія 
уже відбулася, то переоцінити ймовірність кожної гіпотези можна за формулою Бейєса.
Припустимо, що несумісні гіпотези 
складають повну групу подій. Ймовірності цих гіпотез до випробуванні відомі і дорівнюють 
. Проведено випробування, в результаті якого з’явилася подія . Ймовірність гіпотези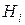 
за умовою з’явлення події визначається формулою
, 
,
де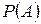 
– повна ймовірність події .
| Приклад 6. | Ймовірність улучення в мішень для першого стрільця дорівнює 0,9, для другого – 0,8. Обидва стрільця виконали по одному пострілу. Визначити ймовірність того, що мішень улучена. |
Розв’язання.
Подія 
– улучення першого стрільця, подія 
– улучення другого стрільця.
, 
.
Подія 
– промах першого стрільця, подія 
– промах другого стрільця.
, 
.
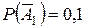Подія – мішень уражена, тобто хоча б один стрілець улучив у мішень.
Подія 
– обидва стрільця промахнулися.
.
Улучення або промахи стрільців незалежні один від одного.
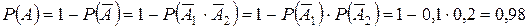
| Приклад 7. | В одній урні 2 білих, 4 синіх і 3 чорних кулі, в другій відповідно 3, 2 і 5 куль. Виймають по одній кулі з кожної урни. Визначити ймовірність того, що вони різнокольорові. |
Розв’язання.
В урнах містяться кулі трьох кольорів. Варіанти різних по кольору куль можуть бути такими:
| 1 урна | б | б | с | с | ч | ч |
| 2 урна | с | ч | б | ч | б | с |
Ймовірність кожного з варіантів визначається за теоремою множення ймовірностей незалежних подій, а загальна ймовірність – їх підсумовуванням.
.
| Приклад 8. | Ймовірність одного улучення в ціль при одному залпі з двох гармат дорівнює 0,44. Знайти ймовірність поразки цілі при одному пострілі першої гармати, якщо відомо, що для другої гармати ця ймовірність дорівнює 0,6. |
Розв’язання.
Позначимо ймовірності улучення 1-ї і 2-ї гармати через 
і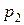 
, тоді ймовірності протилежних подій будуть 
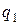і 
, а ймовірність тільки одного улучення виразиться співвідношенням:
; 
,
, 
, 
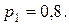
| Приклад 9. | На склад надходять праски з двох заводів, перший з яких поставляє 70%, другий – 30% усієї кількості прасок. Відомо, що перший завод випускає 90% продукції, здатної прослужити гарантійний термін, а другий – 95%. Яка ймовірність, що навмання узята праска прослужить гарантійний термін? |
Розв’язання..
Подія – праска прослужить гарантійний термін.
1. Визначення гіпотез:
гіпотеза 
– праска виготовлена першим заводом,
гіпотеза 
– праска виготовлена другим заводом.
Гіпотези несумісні і утворюють повну групу.
2. Визначення ймовірностей гіпотез до проведення випробування:
; 
. 
.
3. Визначення умовних ймовірностей
; 
.
4. Визначення повної ймовірності
| Приклад 10. | Є 10 урн. У 3-х з них – по 4 білих, 6 чорних куль, у 5-ти – по 7 білих, 3 чорних куль, у 2-х – по 2 білих, 8 чорних куль. Навмання взята куля виявилася білою. Яка ймовірність того, що вона взята з 3-ї групи урн? |
Розв’язання..
В цій задачі потрібно використати формулу Бейєса, тому що результат відомий (куля виявилася білою).
Подія – куля виявилася білою.
1. Гіпотеза – куля взята з першої групи урн.
Гіпотеза – куля взята з другої групи урн.
Гіпотеза 
– куля взята з третьої групи урн.
Гіпотези несумісні і утворюють повну групу.
2. 
; 
; 
; 
.
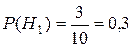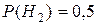3. 
; 
; 
.
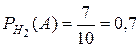4. 
.
5. 
.
Поиск по сайту: