 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Конкретні закони розподілу
Кожен закон розподілу визначається густиною ймовірності, інтегральною функцією, числовими характеристиками та ймовірністю потрапляння на інтервал.
Біноміальний закон – це розподіл ймовірностей, які визначаються за формулою Бернуллі. Він розрахований на дискретні величини і визначається наступними характеристиками
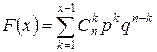 ,
, 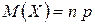
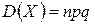 ,
, 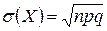
 .
.
Закон Пуассона – це розподіл ймовірностей, які визначаються за формулою Пуассона. Він характеризує дискретні величини і визначається такими величинами:
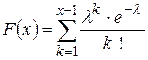 ,
, 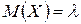 ,
,
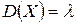 ,
, 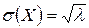 ,
, 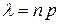 ,
,
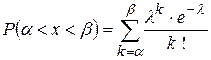 .
.
У цьому законі є характерна особливість:  і
і 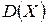 співпадають.
співпадають.
Закон рівномірного розподілу ймовірностей – це такий закон розподілу неперервної випадкової величини, усі значення якої лежать на відрізку 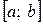 і мають постійну густину ймовірності на цьому відрізку.
і мають постійну густину ймовірності на цьому відрізку.
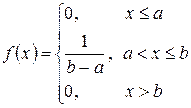
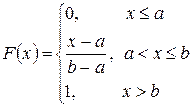
 ,
, 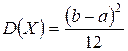 ,
, 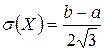 .
.
 .
.
Нормальний розподіл – це розподіл ймовірностей неперервної випадкової величини, що описується диференціальною функцією
 ,
,
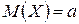 ,
, 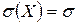 .
.
Інтегральна функція нормального розподілу:
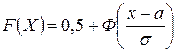 .
.
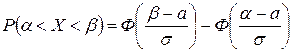 ,
,
де  – функція Лапласа (інтеграл ймовірностей).
– функція Лапласа (інтеграл ймовірностей).
Нормальною кривою називають графік густини нормального розподілу. Ймовірність заданого відхилення  нормально розподіленої випадкової величини від її математичного сподівання:
нормально розподіленої випадкової величини від її математичного сподівання:
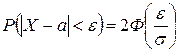 .
.
| Правило “трьох сигм”: | Практично достовірною є подія, яка складається в тому, що абсолютна величина відхилення нормально розподіленої випадкової величини від її математичного сподівання не перевершує потроєного середнього квадратичного відхилення
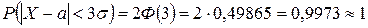 . .
|
Показниковий (експоненціальний) розподіл описується диференціальною функцією
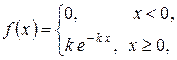
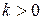 .
.
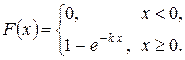
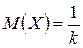 ,
, 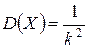 ,
, 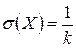 .
.
 .
.
Особливість цього закону: співпадають  і
і 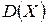 .
.
| Приклад 16. | У цеху 4 мотори. Для кожного мотора ймовірність того, що він включений у даний момент, дорівнює 0,6. Скласти ряд розподілу числа моторів, включених у даний момент. Знайти 
|
Розв’язання.
Випадкова величина  – число включених моторів – може приймати значення 0, 1, 2, 3, 4. Для кожного можливого значення випадкової величини знайдемо ймовірність за формулою Бернуллі:
– число включених моторів – може приймати значення 0, 1, 2, 3, 4. Для кожного можливого значення випадкової величини знайдемо ймовірність за формулою Бернуллі:
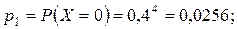
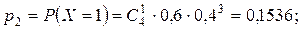
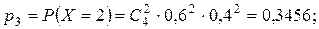

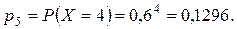
Складемо ряд розподілу:

| |||||

| 0,0256 | 0,1536 | 0,3456 | 0,3456 | 0,1296 |
Перевірка: 0,0256 + 0,1536 + 0,3456 + 0,3456 + 0,1296 = 1.
 =
= 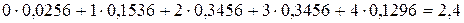 .
.
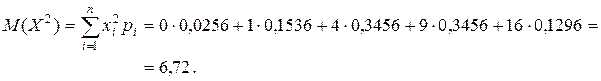
 ;
;  .
.
| Приклад 17. | Дано інтегральну функцію:
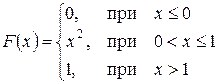 Знайти: а) диференціальну функцію;
б) ймовірність потрапляння випадкової величини в інтервал (1/4; 2/3);
в)
Знайти: а) диференціальну функцію;
б) ймовірність потрапляння випадкової величини в інтервал (1/4; 2/3);
в) 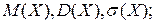 г) побудувати графік
г) побудувати графік 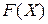 і і 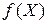 . .
|
Рішення.
а) Знайдемо диференціальну функцію:
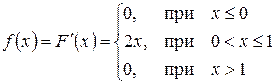
б)  .
.
в) 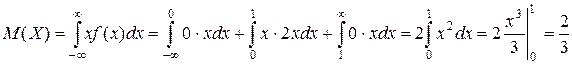 ,
,
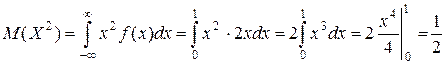 ,
,
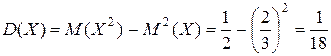 .
.
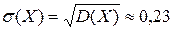 .
.
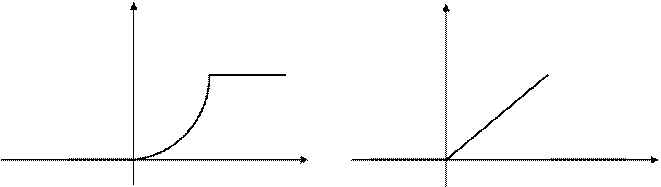
г) графіки функцій  і
і 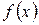 мають вигляд (рис. 1, 2):
мають вигляд (рис. 1, 2):
| 
| 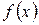
| ||||||||||||||||||||||||||||
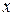
| 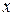
| |||||||||||||||||||||||||||||
Рис. 1 Рис. 2
Поиск по сайту: