Розділ 17.4. Завдання до заняття 17

Теоретичні питання до заняття 17

1. За матеріалом заняття 14 нагадати методику обчислення числових характеристик методом добутків.

2. Записати формулу обчислення вибіркового коефіцієнта кореляції і пояснити її складові.

3. У чому полягає зміст коефіцієнта кореляції і мірою якої величини він служить?

4. Сформулювати методику обчислення вибіркового коефіцієнта кореляції за допомогою умовних варіант.

5. Сформулювати методику побудови рівняння прямої лінії регресії за згрупованими даними.

Індивідуальні завдання до заняття 17

Приклад:

За даними виборок Х і У:

1. Побудувати кореляційну таблицю.

2. Знайти вибірковий коефіцієнт кореляції.

3. Побудувати рівняння прямої.

Рішення

Для побудови кореляційної таблиці розіб’ємо множину значень величин Х і У на інтервали за допомогою формули Стерджесса (дивись заняття 11)

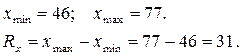
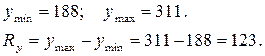
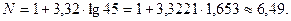
Довжини інтервалів для виборок Х і У:

Складемо кореляційну таблицю 1.

Таблиця 1

Y	X
46-50	50-54	54-58	58-62	62-66	66-70	70-74	74-80
188-206
206-224
224-242
242-260
260-278
278-296
296-314

Перейдемо від інтервалів, до їх середин у стовпці У та рядку Х, тоді таблиця 1 набуде вигляду (таблиця 2):

Таблиця 2

Y	X

Перейдемо до умовних варіант 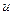і 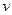, для цього приймемо 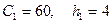і 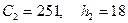, для цього застосуємо формули (17.6). Таблиця 2 в умовних варіантах набуде вигляду (таблиця 3):

Таблиця 3

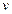
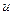
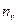
-3	-2	-1
-3
-2
-1

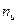
Для обчислення 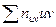складемо розрахункову таблицю 4.

Таблиця 4

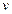
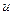
-3	-2	-1
-3	-18 -18	-2 -3							-20
-2		-8 -8							-8
-1			-5 -5	0 -5					-5
				0 0	4 0
					7 7	8 4
							9 6
								4 3
	-18	-11	-5	-5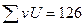

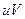
Величини 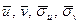можна обчислити методом добутків. Використовуючи таблицю 3 складемо розрахункову таблицю 5.

Таблиця 5

№ п/п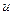
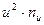
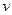
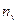
	-3		-18		-3		-21
	-2		-10		-2		-8
	-1		-5		-1		-10
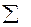
			-1				-19

Знайдемо умовні середні:

Знайдемо умовні дисперсії:

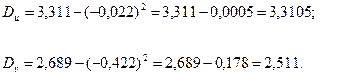
Тоді вибірковий коефіцієнт кореляції обчислюємо за формулою (17.7)

Як видно із значення вибіркового коефіцієнта кореляції, тіснота зв’язку між величинами Х і У досить велика. Знайдемо рівняння прямої лінії регресії У на Х (формула 17.5)

.

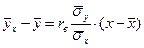Для цього знайдемо 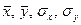методом добутків

.

.

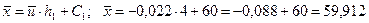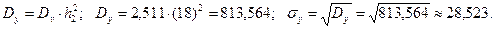
Тоді шукане вибіркове рівняння прямої лінії регресії набуває вигляду

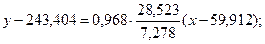
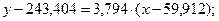
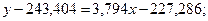
Рекомендована література

1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. – Изд. 7-е, стер. – М.: Высш. шк., 2001. – 479 с.: ил. 2.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике Учеб. пособие для вузов. – Изд. 5-е, стер. – М.: Высш. шк., 2001. – 400 с.: ил.

3. Лавринчук В.П. та інш. Теорія ймовірностей та елементи математичної статистики / Навч. посібник. Чернівці: 1988. – 176 с.

4. Рудавський Ю.К., Костробій П.П., Олексів І.Я. та ін. Збірник задач з теорії ймовірностей / Навч. посібник. Львів: Львівська політтехніка. – 2000. – 242 с.

5. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании / Учебник. – 4-е изд., испр. – М.: Дело, 2003. – 688 с.

6. В.В. Липовик, О.В. Максимов, Л.В. Коломойцева Теорія ймовірностей / підручник – Кривий Ріг: Видавничий дім, 2004 – 247 с.

7. И. Маринеску, Ч. Мойнягу, Р. Никулеску, Н. Ранку В. Урсяну Основы математической статистики и ее приложение. – М.: Статистика, 1970. – 223 с.

8. Вентцель Е.С. Теория вероятностей. – М.: Наука, - 1969. – 112 с.

9. Кремер Н.Ш. Теория вероятностей и математическая статистика/ Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2003. – 543 с.

10. Колмогоров А.Н., Журбенко И.Г., Прохоров А.В. Введение в теорию вероятностей. М.: Наука, 1982. – 160 с.

11. Лихолетов И.И. Высшая математика, теория вероятностей и математическая статистика. Минск: В. школа, 1976. – 720 с.

12. Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики. М.: Высшая школа, 1972. – 480 с.

13. Колде Я.К. Практикум по теории вероятностей и математической статике. – М.: Наука, 1991. – 157 с.

14. Пугачев В.С. Теория вероятностей и математическая статистика. – М.: Наука, 1979. – 496 с.

15. Гусак А.А. Высшая математика. В 2-х т. Т. 2.: Учебник для студентов вузов. – 3-е изд., стереотип. – Мн.: ТетраСистемс, 2001. – 448 с.

16. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. II: Учебн. пособие для втузов. – 5-е изд., испр. – М.: Высш. шк., 1999. – 416 с.: ил.

17. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учебное пособие. – М.: Наука, 1987. – 6000 с.

18. Беляев Б.И., Тавзадзе М.Н. Теория погрешностей и способ найменьших квадратов. – М.: Недра, 1992. – 286 с.

19. Ф. Мостеллер. Пятьдесят занимательных вероятностных задач с решениями. – 2-е изд., исправл. – М.: Наука, 1975. – 112 с.

20. Вирченко Н.А. Математика в афоризмах, цитатах, высказываниях. – К.: Вища школа, 1983. – 278 с.

21. Г. Вилейтнер История математики от Декарта до середины XIX столетия. – 2-е изд. – М.: Наука, 1966. – 508 с.

22. Гришин А.Ф., Кочерова Е.В. Статистические модели: построение, оценка, анализ: Учеб. пособие. – М.: Финансы и статистика, 2005. – 416 с.: ил.

Поиск по сайту: