Багатокритеріальні завдання оптимального керування

Більшість моделей складних систем характеризуються тим, що описувані ними процеси носять динамічний характер, тобто компоненти системи характеризуються величинами, що змінюються в часі. Функцією часу є також і керування в цих системах.

Розглянемо наступну систему керування.

Нехай стан системи описується вектором x E_m. У початковий момент t₀ система перебуває в стані x(t₀) = x⁰. Припустимо, що динаміка зміни компонент системи на відрізку часу [ t₀, T ] описується векторним диференціальним рівнянням:

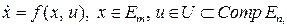(7.1)

де й – керуючий параметр, що має зміст зовнішніх впливів, за допомогою яких відбувається керування розвитком.

Будемо вважати, що параметр і вибирається безупинно в часі функція, що й вийшов у результаті, u ( t ) _, t [ t0, T ], u (t) U, вимірна по t.

Будемо також уважати виконаними всі умови, що гарантують існування, продовжуваність і одиничність рішення диференціального рівняння (7.1) при будь-якому вимірнім керуванні u (t) на відрізку часу [ t₀, Т ] і при початковій умові x (t ₀) = x ⁰. Керування u (t), що є тільки функцією часу, називається програмним.

Кожне програмне керування u (t), t [ t ₀, T ], визначає деяку траєкторію руху x (t), t [ t ₀, T ], одержувану як рішення рівняння (7.1) при початковій умові x (t ₀) = x ⁰.

Позначимо через U безліч припустимих керувань. Вибираючи різні керування з безлічі U, одержимо різні траєкторії. Нехай – безліч досяжності рівняння (7.1), тобто безліч крапок Em, у які може потрапити рішення рівняння (7.1) з початкового стану в момент часу Т при використанні всіляких програмних керувань u (t) U, t [ t ₀, T ]. Іншими словами, безліч досяжності є безліч кінців траєкторій диференціального рівняння (7.1) { х (Т)}, що виходять із початкового стану х ⁰ при всіляких програмних керуваннях u (t) U, t [ t ₀, T ].

Припустимо далі, що якість траєкторії визначається крапкою х (Т), у яку переходить система в результаті цього розвитку в кінцевий момент Т. Таким чином, будемо вважати, що на безлічі досяжності заданий векторний критерій Н (х (Т)), x (T) , що визначає якість траєкторії x (t) і відповідного керування u (t). Приходимо до динамічної багатокритеріальної задачі оптимізації, у якому безліч варіантів рішення або результатів позначимо:

(7.2)

а безліч оцінок буде мати вигляд

(7.3)

Безлічі й залежать від параметрів х ⁰, t ₀ початкові умови, що представляють собою, для завдання (7.1). Оскільки рішення сформульованої динамічної багатокритеріальної задачі оптимізації залежить від x ⁰, T – t ₀, будемо позначати її через Г(x ⁰, T – t ₀).

Отже, ми маємо динамічну багатокритеріальної задачі оптимізації Г(x ⁰, T – t ₀), безліч усіляких результат (x ⁰, T – t ₀), певних в (7.2), і безліч усіляких оцінок (x ⁰, T – t ₀), певних в (7.3). Нехай дані – безліч ефективних оцінок (Парето-Оптимальних), – безліч слабо ефективних оцінок (оптимальних по Слейтеру) і – відповідні безлічі оптимальних керувань.

Нехай u (t) – деяке оптимальне керування, a x (t) – відповідна до цього керування оптимальна траєкторія. Розглянемо в кожний момент часу t [ t ₀, T ] завдання багатокритеріальної оптимізації з початковими умовами t, x (t), яку позначимо через Г( (t), T − t).

У загальному випадку траєкторія x (τ), t ≤ τ ≤ T не обов'язково є оптимальною в завданні Г( (t), T − t). Така властивість оптимальних рішень називається динамічною нестійкістю. З іншого боку, якщо x (τ) є оптимальною траєкторією в поточнім завданні багатокритеріальної оптимізації Г( (t), T − t) t [ t ₀, T ], те оптимальне керування u (t) і траєкторію x (t) називають динамічно стійкими.

Якщо динамічно стійкими виявляються всі оптимальні керування, то говорять про динамічну стійкість рішення й принципу оптимальності.

Питання динамічної стійкості тісно пов'язаний з вибором принципу оптимальності. Існує цілий ряд принципів оптимальності, для яких оптимальні рішення виявляються динамічно стійкими. До таких принципів ставляться оптимальність по Парето й Слейтеру, рівновага по Нешу й ряд інших. Існують також принципи оптимальності, які не мають властивість динамічної стійкості.

Оптимальність по Парето – такий стан системи, при якім значення кожного приватного критерію, що описує стан системи, не може бути поліпшене без погіршення положення інших елементів.

Безліч станів системи, оптимальних по Парето, називають «безліччю Парето», «безліччю альтернатив, оптимальних у змісті Парето», або «безліччю оптимальних альтернатив».

Ситуація, коли досягнута ефективність по Парето – це ситуація, коли всі вигоди від обміну вичерпані.

Оптимум по Парето говорить, що позитивний стан досягає максимуму, а розподіл ресурсів стає оптимальним, якщо будь-яка зміна цього розподілу погіршує стан хоча б одного елемента системи.

У рамках даної роботи видно динамічну стійкість Парето-Оптимальних рішень. Дійсно, нехай Парето Оптимальна безліч оцінок і – Парето-Оптимальна безліч рішень (керувань) у багатокритеріальної динамічному завданню оптимізації Г(x ⁰, T – t ₀) для початкового стану x ⁰ із запропонованою тривалістю T – t 0. Нехай { Hi *}= H * – вектор оцінок з безлічі . Припустимо, що обрані керування u (t) і відповідна траєкторія x (t), при яких наприкінці процесу реалізується оцінка H * = { Hi *}. Це означає, що керування u (t) таке, що x (t) у момент часу Т (у момент закінчення процесу) проходить через крапку х (Т), у якій Н (х (Т)) = { Hi (x (T))} так само як раз вектору корисності H *={ Hi *}. Нехай – безліч досяжності керованої системи з початкового стану x 0. Розглядаючи зміну цієї безлічі уздовж траєкторії x (τ), можна помітити, що:

(7.4)

з (7.4) маємо

(7.5)

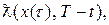
Оскільки вектор H *={ Hi *} належить Парето-Оптимальній безлічі, то не існує такого вектора H '≠ H *, що належить що для всіх i = l, 2,..., п. Тому з (7.5) випливає, що тим більше це має місце для безлічі . Отже, вектор оцінок H *={ Hi *} не домінується жодним з векторів безлічі 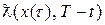, або, що те ж, належить Парето-Оптимальній безлічі поточного завдання з початковою умовою х (τ) і тривалістю . Таким чином, вектор H * у всіх поточних завданнях залишається Парето-оптимальних при русі системи уздовж оптимальної траєкторії х (τ). Оскільки вектор корисності Н * був обраний довільно з безлічі , те це означає динамічну стійкість будь-якого Парето-Оптимального рішення, а отже, і Парето-оптимальної безлічі в цілому.

Запитання для самоперевірки

1. Дайте характеристику багатокритеріальних системам керування.

2. Дайте визначення поняттям альтернатива та принцип оптимальності.

3. Охарактеризуйте основні завдання оптимального керування.

4. Опишіть багатокритеріальні завдання оптимального керування.

5. Охарактеризуйте динамічну стійкість Парето-оптимальних рішень.

Поиск по сайту: