 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Класифікація систем
Існує цілий ряд різних класифікацій систем, що відбивають ті чи інші їх властивості. Така різноманітність зумовлена розбіжністю цілей класифікації й багатогранністю властивостей систем.
Віднесення об'єкта до того чи іншого класу часто викликає проблеми, що можуть бути пов'язані з розмитістю меж класів, недостатньою вивченістю системи й іншими причинами. Одна з основних проблем класифікації – це проблема повноти. Тому часто вводять такі класи, як “змішаний”, “усе інше” і т. п. У таблиці 3.1 наведено класифікацію систем за певними ознаками. Додамо, що перелік ознак може бути доповнений.
Розрізняють реальні та абстрактні системи. До реальних належать ті, що реально існують у природі, техніці або суспільстві. Наприклад, реальними є Сонячна система, прокатний стан, Україна як держава. Прикладами абстрактних систем можуть бути ідеальні відображення реальних систем та процесів (карти місцевості, технічні креслення тощо), а також інші ідеальні конструкції (системи рівнянь, алгоритми та інші).
Для реальної системи може бути побудована певна множина моделей, що розрізняються за метою дослідження, необхідним ступенем деталізації та іншими ознаками.
Наприклад, реальна локальна обчислювальна система, з погляду системного адміністратора, є сукупністю програмного, математичного, інформаційного, лінгвістичного, технічного й іншого видів забезпечення, з погляду користувача, – це сукупність об'єктів, з якими можна обмінюватися інформацією, з погляду технічного обслуговування, – сукупність справних і несправних засобів.
Таблиця 3.1.
| № | Класифікаційна ознака | Тип системи |
| 1. | Природа елементів | Реальні (фізичні) Абстрактні |
| 2. | Походження | Природні Штучні Змішані |
| 3. | Тип змінних | З якісними змінними З кількісними змінними Зі змішаним описом змінних |
| 4. | Тип оператора системи | Чорний ящик Непараметричний клас Параметричний клас Білий ящик |
| 5. | Термін існування | Сталі Тимчасові |
| 6. | Мінливість властивостей | Статичні Динамічні |
| 7. | Ступінь складності | Прості Складні Великі |
| Відношення до зовнішнього середовища | Закриті Відкриті | |
| Реакція на вплив, що збурює | Активні Пасивні |
Продовження таблиці 3.1.
| № | Класифікаційна ознака | Тип системи |
| 10. | Характер управління | Керовані зовні Самокеровані З комбінованим управлінням Без управління |
| 11. | Ступінь організованості | Добре організовані Погано організовані (дифузні) Ті, що саморганізуються |
| 12. | Ступінь участі та впливу людини | Технічні Людино-машинні Організаційні |
Природні та штучні об'єкти, які відображуються у свідомості людини, виступають у ролі абстракцій, понять, що утворюються шляхом мисленевого висвітлення тих чи інших сторін цих об’єктів. Вони не мають прямих аналогів у реальному світі. Абстрактні проекти створюваної системи втілюються в реально існуючу, яку можна відчути, а при її вивченні знову відбити у формі абстрактної.
Розглядаючи системи за класифікаційною ознакою походження, можемо побачити, що у кожному типі систем можна виділити певні класи (рис. 3.1).
Нижче (рис. 3.2) наведено схему класифікації за типом змінних, що описують вхід і вихід системи.

Рис. 3.1.
Якісні й кількісні змінні потребують принципово різних підходів до їх обробки й аналізу. Клас систем зі змішаним описом змінних на першому рівні утворюють системи, для яких частина змінних має кількісний опис, а частина – якісний. На другому рівні до підкласу змішаних систем включено системи з якісними змінними, частина з яких описується змістовно, а частина – формалізовано. До аналогічного підкласу систем з кількісними змінними віднесено системи, у яких частина змінних є дискретними, а частина – неперервними. На третьому рівні до підкласу змішаних систем включено системи, у яких є змінні принаймні двох з виділених типів (детерміновані, стохастичні чи розпливчаті).
У наведеній класифікації другий рівень для систем з якісно-кількісним описом змінних є об'єднанням відповідних рівнів перших двох класів систем. Третій рівень є однаковим для всіх підкласів систем з якісним описом змінних.
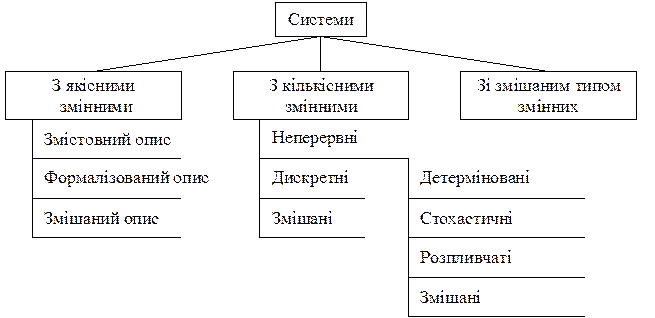
Рис. 3.2.
Класифікація за типом оператора (Рис. 3.3) поділяє системи за характером зв'язку між вхідними й вихідними змінними. На першому рівні характеристичною ознакою є ступінь повноти інформації про цей зв'язок.
Перший клас утворюють системи типу чорного ящика. Для таких систем немає ніякої інформації про характер зв'язку між вхідними й вихідними змінними. Для непараметризованих систем, що становлять другий клас, є уривчаста інформація про характер цього зв'язку.
Зокрема, може бути відомо, що оператор зв'язку має такі властивості, як гладкість, симетричність, неперервність, монотонність і т. п. До третього класу належать параметризовані системи. Для них оператор зв'язку відомий з точністю до значень параметрів, які до нього входять. Наприклад, може бути встановлено, що зв'язок між входом і виходом описується рівнянням виду Y=AX + B. Але при цьому є невідомими значення параметрів А і В. Нарешті, четвертий клас утворюють системи типу білого ящика, тобто такі, для яких зв'язок між входом і виходом є повністю описаним.

Рис. 3.3.
За терміном існування системи поділяють на сталі й тимчасові. До сталих зазвичай відносять ті, що зберігають свою цілісність протягом часу, який цікавить дослідника. Це велика кількість природних (Всесвіт, Земля, стійки елементарні частинки й атоми тощо) та штучних (ювелірні вироби, архітектурні та гідротехнічні споруди тощо) систем, які протягом певного часу функціонування практично не змінюються. Тимчасовими є системи, час існування яких є порівняним або навіть меншим, ніж час, потрібний для їх дослідження.
Спостереження мінливості властивостей дає змогу поділити системи на статичні та динамічні. До статичних відносять ті, при дослідженні яких можна нехтувати змінами їх характеристик та суттєвих властивостей у часі. Тобто у процесі дослідження систему можна вважати такою, що має лише один можливий стан.
На відміну від статичних, динамічні системи мають кілька можливих станів. З часом система може переходити з одного стану до іншого безупинно або тільки в деякі дискретні моменти.
Розподіл систем на прості, складні й великі підкреслює, що в системному аналізі розглядаються не будь-які, а саме складні системи великого масштабу. При цьому виділяють структурну й функціональну (обчислювальну) складність.
Загальновизнаної межі, яка розділяла б прості, великі й складні системи, немає. Однак умовно будемо вважати, що складні характеризуються трьома основними ознаками: властивістю робастності, наявністю неоднорідних зв'язків і емерджентністю.
Під робастністю розуміють здатність системи зберігати часткову працездатність (ефективність) при відмові її окремих елементів чи підсистем. Вона зумовлюється функціональною надмірністю складної системи й виявляється в зміні ступеня деградації виконуваних функцій, що залежить від глибини збуджуючих дій. Проста система може знаходитися не більше ніж у двох станах: повної працездатності (справному) або повної непрацездатності (несправному).
У складних системах, крім значної кількості елементів, присутні численні й різні за типами (неоднорідні) зв'язки між елементами. Основними є такі види зв'язків: структурні (у тому числі ієрархічні), функціональні, каузальні (причинно-наслідкові, відносини істинності), інформаційні, просторово-часові. За цією ознакою будемо відрізняти складні системи від великих систем, що є сукупністю однорідних елементів, об'єднаних зв'язком одного типу.
Складна система має властивості, відсутні у кожного з її компонентів. Це називають інтегративністю (цілісністю), чи емерджентністю системи.
Одну з найбільш повних і цікавих класифікацій за рівнями складності запропонував К. Боулдинг. Виділені в ній рівні наведено в таблиці 3.2.
Таблиця 3.2.
| Тип системи | Рівень складності | Приклади |
| Неживі системи | Статичні структури або кістяки. Прості динамічні структури із заданим законом поведінки (спрямування). Кібернетичні системи з керованими циклами зворотного зв'язку | Кристали Годинниковий механізм Термостат |
| Живі системи | Відкриті системи зі структурою, яка само зберігається (перший щабель, на котрому можливий поділ на живе і неживе). Живі організми з низькою здатністю сприймати інформацію. Живі організми з більш розвинутою здатністю сприймати інформацію, але такі, що не мають самосвідомості. Системи, що характеризуються самосвідомістю, мисленням і нетривіальною поведінкою. Соціальні системи Трансцендентні системи або системи, що є на сьогодні поза нашим пізнанням | Клітини, гомеостат Рослини Тварини Люди Соціальні організації |
У цій класифікації, як правило, кожен наступний клас містить у собі попередній, характеризується великим проявом властивостей відкритості та стохастичності поведінки, більш яскраво вираженими закономірностями ієрархічності й історичності (аналізованих нижче), хоча це не завжди зазначається, а також більш складними механізмами функціонування й розвитку.
При класифікації систем за способом управління (Рис. 3.4) на першому рівні визначається місце розташування керуючої системи (поза чи всередині керованої системи). Можливий також випадок комбінованого управління, коли частина керуючої системи знаходиться всередині керованої системи, а інша частина – поза нею.

Рис. 3.4.
На другому рівні незалежно від місця розташування блоку управління розподіл систем здійснюється за ступенем визначеності траєкторії (у фазовому просторі), що приводить систему до мети, і здатності блоку управління утримувати систему на цій траєкторії. Перший підклас у всіх випадках утворюють системи, у яких точно відомо траєкторію, а також те, як треба впливати на систему для досягнення мети. Прикладами систем, що відносяться до цього підкласу (системи без зворотного зв’язку, самокеровані та автоматичні системи), можуть служити телефон-автомат, робота ЕОМ за заздалегідь заданою програмою, ріст зародка живого організму і т. п.
Набагато частіше зустрічається ситуація, коли система сходить із заданої траєкторії внаслідок того, що процеси на некерованих входах відрізняються від передбачуваних, або під впливом випадкових і невраховуваних факторів. Якщо відхилення системи від заданої траєкторії невелике, то застосовується спосіб управління, названий регулюванням. У цьому разі знаходять різницю між поточною та заданою траєкторіями y (t) – y0 (t) і визначають додаткові керівні впливи, здатні в найближчому майбутньому повернути виходи системи на задану траєкторію. Регульовані системи виділені в другий підклас усіх розглянутих класів. До них, зокрема, належать автопілоти літаків, рефлекторні реакції тварин, верстати, керовані операторами тощо.
Наступний спосіб управління застосовують, якщо відхилення від заданої траєкторії занадто великі, і повернути систему на цю траєкторію методами регулювання неможливо, а також у випадках, коли з якихось причин не можна задати опорну траєкторію. Управління в таких ситуаціях може полягати в тому, щоб спрогнозувати поточну траєкторію y (t) і підібрати такі параметри системи, за яких прогнозована траєкторія в певний момент часу потрапить до заданої цільової області Y*. Такому способу управління відповідає третій підклас. Прикладами його реалізації є процеси адаптації живих організмів до умов середовища, що змінюються, робота пілотів літаків, автоматизовані системи управління тощо.
Можлива також ситуація, коли траєкторія даної системи ні за яких значень параметрів не перетинає цільову область. У цьому разі ціль може бути досягнута шляхом зміни структури системи. Відповідний спосіб управління називають структурною адаптацією, а системи, у яких він реалізується, утворюють четвертий підклас. Прикладами можуть служити гнучкі автоматичні виробництва, обчислювальні мережі, сільськогосподарські машини зі змінними начіпними та причіпними пристроями, видоутворення в живій природі, утворення й розпад держав тощо.
Уперше поділ систем за ступенем організованості за аналогією до класифікації проблем Г. Саймона і А. Нєлла (добре структуровані, погано структуровані та неструктуровані проблеми) запропонував В.В. Налімов, який виділив класи добре організованих (аналізованих іноді в літературі окремо як класи саморегульованих, самонаучуваних, самоналагоджуваних і т. п. систем) та погано організованих (або дифузійних) систем. Якщо додати до цих двох класів ще системи, що саморганізуються, то отримані класи можна достатньо чітко розмежувати за допомогою характерних для кожного з них ознак, які дають можливість поставити у відповідність класу певні методи формалізованого подання систем і засоби подання цілей у них. Виділені класи можна розглядати як підходи до відображення об'єкта або розв'язуваної задачі, що можуть вибиратися залежно від стадії пізнання об'єкта й можливості одержання інформації про нього.
Коротко охарактеризуємо ці класи.
1. Відобразити аналізований об'єкт або процес ухвалення рішення у вигляді добре організованої системи означає визначити елементи системи та їх зв'язки між собою і з цілями системи. У цьому разі завдання вибору цілей і засобів їх досягнення (елементів, зв'язків) не розділяються. Проблемна ситуація може бути описана у вигляді виразу, що пов'язує ціль із засобами, тобто, у вигляді критерію або показника ефективності, критерію функціонування, цільової функції й т. п., що можуть бути подані складним рівнянням, формулою, системою рівнянь. Часто при цьому говорять, що ціль рекомендується як критерій ефективності або критерій функціонування, хоча насправді в подібних виразах об'єднані й ціль, і засоби.
Більшість моделей фізики й технічних наук засновані на відображенні об'єктів і процесів як добре організованих систем. Наприклад, роботу складного механізму подають у вигляді спрощеної схеми або системи рівнянь, які враховують не всі, а найбільш істотні з погляду його призначення елементи та зв'язки між ними. Атом часто описують як планетарну систему, яка складається з ядра та електронів. Це суттєво спрощує реальну картину, але є достатнім для розуміння багатьох властивостей атома.
Неважко помітити, що для відображення об'єкта у вигляді добре організованої системи слід виділяти істотні та не зважати на несуттєві для конкретної цілі розгляду компоненти. За необхідності більш детального опису потрібно уточнити ціль, вказавши, з яким ступенем глибини нас цікавить досліджуваний об'єкт, і побудувати нову систему, що відображає його, беручи до уваги внесені корективи. Наприклад, при описі будови атома можна врахувати склад ядра, квантово-механічні закономірності поведінки електронів та ядер, магнітні властивості тощо.
Відображення об'єкта у формі добре організованої системи використовують у тому разі, коли можна запропонувати детермінований опис і експериментально обґрунтувати правомірність його вживання, тобто, адекватність моделі реальному об'єкту чи процесу. Спроби застосувати клас добре організованих систем для відображення складних багатокомпонентних об'єктів або для розв’язування багатокритеріальних задач, що виникають, наприклад, при удосконалюванні управління й розробці АСУ, вдаються погано. Це не тільки потребує неприпустимо великих витрат часу на одержання й опрацювання моделей, а й часто практично не може бути реалізованим, оскільки не вдасться поставити експеримент, що доводить правомірність застосування запропонованих аналітичних залежностей. Тому здебільшого при дослідженні складних об'єктів на початковому етапі постановки задач їх відображають класами, які характеризуються далі окремо.
2. При відображенні об'єкта у вигляді погано організованої, або дифузійної, системи не ставиться завдання визначити всі компоненти, їх властивості та зв'язки між ними й цілями системи. Система характеризується певним набором макропараметрів та зв’язків між ними або закономірностями, що виявляються на основі дослідження визначеної за допомогою деяких правил достатньо представницької вибірки компонентів, що характеризують досліджуваний об'єкт або процес.
У першому випадку поведінка системи може бути детермінованою, тобто, знання певних характеристик системи дає змогу однозначно встановити її інші суттєві властивості. У другому випадку на основі вибіркового дослідження компонентів одержують їх статистичні характеристики або закономірності поведінки і поширюють отримані результати на всю систему в цілому. При цьому робляться відповідні застереження. Наприклад, при одержанні статистичних закономірностей їх поширюють на поведінку всієї системи, вказуючи рівень значущості (ймовірність помилки), довірчі межі тощо.
Прикладом дифузійної системи є газ. Його поведінка не може бути визначена шляхом повного й точного опису поведінки всіх його молекул, тому його характеризують або макропараметрами (параметрами стану) – тиском, температурою, об’ємом тощо, або функціями розподілу мікропараметрів – швидкостей молекул, їх кінетичних та потенціальних енергій та інших. Базуючись на цих параметрах, розробляють прилади й устрої, що використовують властивості газу, не досліджуючи при цьому поведінки кожної окремої молекули.
Відображення об'єктів у вигляді дифузійних систем знаходить широке застосування при визначенні пропускної спроможності систем управління, кількості працівників в обслуговуючих, наприклад, ремонтних, цехах підприємств і в обслуговуючих установах (для вирішення подібних задач використовують методи теорії масового обслуговування), при дослідженні документальних потоків інформації тощо.
3. Відображення об'єктів у вигляді систем, що саморганізуються, або розвиваються, дає змогу досліджувати найменш вивчені об'єкти та процеси з великою невизначеністю на початковому етапі постановки завдань. Такі системи мають ознаки, характерні для дифузійних систем: стохастичність поведінки, нестабільність окремих параметрів і, крім того, такі специфічні риси, як непередбачуваність поведінки; здатність адаптуватися до умов динамічного середовища; змінювати структуру, зберігаючи при цьому властивість цілісності; протистояти ентропійним тенденціям; формувати можливі варіанти поведінки й вибирати серед них найкращий; а також інші ознаки, що наближають їх до реальних об'єктів.
Сказане означає, що моделі систем, які саморганізуються, або розвиваються, мають надавати можливість відображення розглянутих властивостей. При їх формуванні змінюється звичне уявлення про моделі, характерне для математичного моделювання та прикладної математики. Стають інакшими також уявлення про доведення адекватності моделей.
Основну конструктивну ідею, завдяки якій можливо реалізувати відображення об'єкта класом систем, що саморганізуються, можна сформулювати в такий спосіб. Розробляють знакову систему, за допомогою якої фіксують відомі на даний момент компоненти та зв'язки. Потім через перетворення отриманого відображення, використовуючи встановлені правила (правила структуризації, або декомпозиції, правила композиції), одержують нові, не відомі раніше взаємовідносини й залежності, що можуть або послужити основою прийнятих рішень, або підказати наступні кроки на шляху підготування рішення.
Таким чином, можна накопичувати інформацію про об'єкт, фіксуючи при цьому всі нові компоненти та зв'язки (правила взаємодії компонентів), і, застосовуючи їх, одержувати відображення послідовних станів системи, що розвивається, поступово створюючи все більш адекватну модель реального досліджуваного або проектованого об'єкта. При цьому інформація може надходити від спеціалістів різноманітних галузей знань і накопичуватися. Адекватність моделі також доводиться послідовно шляхом оцінювання правильності відображення у знаковій моделі компонентів і зв'язків, необхідних для досягнення поставленої цілі дослідження або створення об'єкта.
Практична реалізація побудови такої моделі пов'язана з необхідністю розробки комп’ютеризованих систем автоматизованого проектування, підтримки прийняття рішень, управління тощо, а також відповідних мов. В основу останніх може бути покладений один із методів моделювання систем, наприклад, теорія множин, математична логіка, математична лінгвістика, імітаційне динамічне моделювання і т. п., але в міру розвитку моделі ці методи можуть змінюватися. При моделюванні найбільш складних процесів, таких як цілеутворення, удосконалювання організаційних структур систем управління тощо, “механізм” розвитку (самоорганізації) може бути реалізований у формі відповідної методики системного аналізу.
Іноді аналізований клас систем розбивають на підкласи, виділяючи адаптивні системи, або системи, що самопристосовуються, самонавчаються, самовідновлюються чи самовідтворюються, й інші класи, які відповідають різноманітним властивостям системи, що розвивається. При поданні відображуваного об'єкта у вигляді системи, що саморганізуються, завдання визначення цілей і вибору засобів, як правило, відокремлюються. При цьому завдання вибору цілей, у свою чергу, може бути описане як система, що саморганізуєтеся. Наприклад, при побудові автоматизованої системи управління її мета й завдання не є сталими, а змінюються з часом у міру розвитку системи, якою керують, технічних та програмних засобів управління тощо.
Розглянуті класи систем зручно використовувати як підходи на початковому етапі моделювання будь-якої задачі. Цим класам поставлені у відповідність методи формалізованого відображення систем.
Поиск по сайту: