 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Умовна ймовірність
Означення: Умовною ймовірністю  називають ймовірність події В, обчислену в припущенні, що подія А вже відбулася.
називають ймовірність події В, обчислену в припущенні, що подія А вже відбулася.
 Наприклад:
Наприклад:
У ящику 3 стандартні і 3 браковані деталі. З ящика два рази вилучають по одній деталі. Знайти ймовірність появи стандартної деталі при другому випробуванні (подія В), якщо при першому випробуванні було вилучено браковану деталь (подія А)
Рішення
 .
.
 Теорема: Ймовірність сумісної появи двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, обчислену в припущенні, що перша подія вже відбулася
Теорема: Ймовірність сумісної появи двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, обчислену в припущенні, що перша подія вже відбулася
 . (2.4)
. (2.4)
Наслідок: Ймовірність сумісної появи декількох подій дорівнює добутку ймовірності однієї з них на умовні ймовірності всіх інших, причому ймовірність кожної наступної події обчислюється в припущенні, що всі попередні події вже відбулися.
 . (2.5)
. (2.5)
Порядок, за яким розташовано події, може бути довільним, тобто не має значення яку подію вважати першою, другою і т.п.
 Приклад:
Приклад:
В урні 5 білих, 4 чорних і 3 синіх кульки. Кожне випробування полягає у вилученні навмання однієї кульки, не повертаючи її назад. Знайти ймовірність того, що при першому випробуванні з’явиться біла кулька (подія А), при другому – чорна (подія В) і при третьому – синя (подія С).
Рішення
 .
.
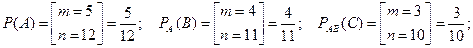

 Означення: Подія В називається незалежною від події А, якщо поява події А не змінює ймовірності появи події В, тобто якщо умовна ймовірність події В дорівнює її безумовній ймовірності
Означення: Подія В називається незалежною від події А, якщо поява події А не змінює ймовірності появи події В, тобто якщо умовна ймовірність події В дорівнює її безумовній ймовірності  , тобто поява події А не залежить від появи події В.
, тобто поява події А не залежить від появи події В.
Теорема: Ймовірність сумісної появи двох незалежних подій дорівнює добутку ймовірностей цих подій
 . (2.6)
. (2.6)
Практично про незалежність подій судять із змісту задачі. Наприклад, ймовірність влучення кожної з двох гармат не залежить від того, чи влучила інша гармата, тому подія “перша гармата влучила” і подія “друга гармата влучила” є незалежними.
 Приклад:
Приклад:
1. Нехай в кожному з трьох ящиків знаходиться по 10 деталей. У першому – 8, у другому – 7 і у третьому – 9 стандартних деталей. З кожного ящика навмання вилучили по одній деталі. Знайти ймовірність того, що всі три деталі, що вилучено, будуть стандартними.
Рішення
Подія А – з першого ящика вилучили стандартну деталь.
Подія В – з другого ящика вилучили стандартну деталь.
Подія С – з третього ящика вилучили стандартну деталь.
Оскільки події є незалежними, то 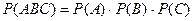


2. Ймовірність появи кожної з трьох незалежних подій  відповідно дорівнюють
відповідно дорівнюють  . Знайти ймовірність появи тільки однієї з цих подій.
. Знайти ймовірність появи тільки однієї з цих подій.
Рішення
Подія  - з’явиться подія
- з’явиться подія  і одночасно не з’являться події
і одночасно не з’являться події  і
і  .
.
Подія 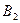 - з’явиться подія
- з’явиться подія  і одночасно не з’являться події
і одночасно не з’являться події  і
і  .
.
Подія  - з’явиться подія
- з’явиться подія  і одночасно не з’являться події
і одночасно не з’являться події  і
і  .
.



Подія А – поява однієї з подій  .
.
 .
.
Поиск по сайту: