 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Знаходження параметів лінійного рівняння регресії методом найменших квадратів
Статистичний аналіз зв’язку між факторною змінною х і результативною змінною у починають із вибору загального типу чи класу рівнянь, які достатньо точно відображають даний зв’язок. При аналізі соціально-економічних і науково-технічних проблем досить часто зустрічаються саме лінійні зв’язки і залежності, тобто зв’язки між досліджуваними ознаками досить точно описуються лінійними моделями.
Будемо вважати, що зв’язок між ознаками х та у є лінійним і описується лінійним рівнянням регресії
y =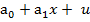 
де у – результуюча змінна;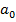 
, 
– параметри рівняння регресії; х – факторна змінна, 
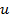– випадкова величина.
Рівняння, яке аналітично моделює залежність середньої величини результуючої ознаки від факторної змінної, називається рівнянням регресії.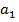 
у цьому рівнянні називається коефіцієнтом регресії, 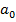– вільним членом рівняння регресії.Лінійне рівняння регресії на графіку зображується прямою лінією, в якій коефіцієнт регресії є кутовим коефіцієнтом (тангенсом кута нахилу прямої до осі ОХ).
Вільний член рівняння регресії 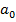відображає довжину відрізка осі ординат від початку координат до перетину з прямою регресії.
Для знаходження прямої, яка б найкраще відображала закономірність зв’язку середнього значення результуючої змінної з факторною, потрібно обгрунтувати певний критерій, який би задовільняла дана пряма. Оскільки пряма регресії повинна знаходитись якнайближче до всіх точок із координатами (хі;уі), то на прктиці найчастіше використовують метод найменших квадратів (МНК).
Згідно з цим методом найменше значення суми квадратів відхилень заданих значень результуючої змінної уі від знайдених за рівнянням регресії теоретичних значень 
. МНК має суттеву перевагу перед іншими відомими методами знаходження прямої регресії, якщо відхилення уі -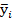 
утворюють нормальний розподіл. На практиці досліджувані сукупності змінних є, зазвичай, нормально розподіленими.
В рівнянні 
0, 1 і 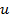є невідомими. Величину 
крім того, важко досліджувати, оскільки вона набуває різних значень для кожного спостередження у. У той же час 0, 1 залишаються постійними і, хоча ми не можемо знайти їх точні значення без вивчення всіх можливих співвідношень між х та у, ми можеио на основі заданих значень спостережень одержати оцінци 
0, 1, параметрів 0, 1.
Нам необхідно знайти рівняння регресії
,
де 
– теоретичні середні значення результуючої змінної для заданого значення хі, коли
0, 1 є відомими. Останнє рівняння в статистиці називають рівнянням прогнозування, оскільки підставляючи в це рівняння конкретне значення факторної змінної х, маємо змогу знайти відповідне «істинне» значення у. Надалі будемо опускати випадкову величину u 
в першому рівнянні і розглянемо друге рівняння.
Нехай ми маємо множину із n спостережень
(х1,у1), (х2,у2),..., (хn,уn).
Умова методу квадратів для знаходження параметрів a0, 1 має вигляд
Q = 
min
Для знаходження параметрів 0 і 1 підставимо рівняння прямої
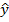= 0 + 1 х
у попередній вираз. У результаті одержимо
Q =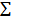 
(у – 0 – 1 х)2. (4)
Як відомо, функція Q набуває мінімальних значень за умови, якщо відповідні часткові похідні дарівнюють нулю.
= 0; 
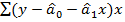= 0
= 0
Розв’язуючи систему, ми одержуємо загальний вигляд формул для обчислення коефіцієнтів 0 і 1
1 = 
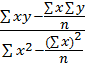
0 =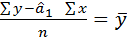 
- 
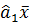
Для визначення рівняння регресії за останніми формулами потрібно мати такі величини
, 
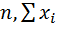Поиск по сайту: