 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Поняття гетероскедастичності
Припущення, які були зроблені при оцінюванні параметрів моделі 1МНК, на практиці можуть порушуватися.
Розглянемо особливості економетричного моделювання, коли порушується умова, згідно з якою припускається, що відхилення мають такий розподіл імовірностей, який зберігається для всіх спостережень. Тоді дисперсія залишків лишається незмінною для кожного спостереження.
Якщо дисперсія залишків стала для кожного спостереження, тобто 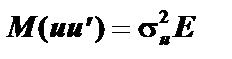 , то ця її властивість називається гомоскедастичністю.
, то ця її властивість називається гомоскедастичністю.
Часто у практичних дослідженнях явище гомоскедастичності порушується. Випробування на наявність чи відсутність гомоскедастичності звичайно не практикується, але здебільшого можна висунути гіпотези про правдоподібність альтернативних припущень щодо пропорційності помилки до X. Так, наприклад, при побудові економетричної моделі, що характеризує залежність між заощадженнями і доходами населення на підставі теоретичної та практичної інформації, можна висунути гіпотезу, що дисперсія залишків за окремими групами населення змінюватиметься і буде пропорційною до середнього доходу цієї групи. Коли розглядати економетричну модель, що характеризує залежність між дивідендами і розміром прибутку або між витратами на харчування і доходом на одного члена сім’ї, витратами на харчування і загальними витратами, то також можна припустити, що дисперсія залишків для окремих груп спостережень змінюватиметься. У цих залежностях пояснювальна змінна може різко змінюватись, а динаміка залежної змінної буде досить помірною, не адекватною до зміни пояснювальної змінної. Це і приводить до зміни дисперсії залишків кожного спостереження або груп спостережень.
Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, тобто, то це явище називається гетероскедастичністю*.
Якщо існує гетероскедастичність залишків, то це спричинюється до того, що оцінки параметрів моделі 1МНК будуть незміщеними, обгрунтованими, але неефективними. При цьому формулу для стандартної помилки оцінки, строго кажучи, застосувати не можна.
припустимо, що дисперсія залишків для моделі  пропорційна до величини Х. Тоді доцільно виконати перетворення вихідної інформації, поділивши, наприклад, усі змінні на Х. Модель набере вигляду
пропорційна до величини Х. Тоді доцільно виконати перетворення вихідної інформації, поділивши, наприклад, усі змінні на Х. Модель набере вигляду
 .
.
У результаті для оцінювання параметрів можна застосувати 1МНК. Зауважимо, що параметри а 0 і а 1 помінялися ролями. Вільним членом моделі замість а 0 став параметр а 1.
Приклад. побудуємо економетричну модель, що характеризує залежність між заощадженнями та доходом населення, млрд ф.ст.
Таблиця
| Рік | |||||||||
| Заощадження | 0,36 | 0,2 | 0,08 | 0,20 | 0,10 | 0,12 | 0,41 | 0,50 | 0,43 |
| Дохід | 8,8 | 9,4 | 10,0 | 10,6 | 11,0 | 11,9 | 12,7 | 13,5 | 14,3 |
| Рік | |||||||||
| Заощадження | 0,59 | 0,90 | 0,95 | 0,82 | 1,04 | 1,53 | 1,94 | 1,75 | 1,99 |
| Дохід | 15,5 | 16,7 | 17,7 | 18,6 | 19,7 | 21,1 | 22,8 | 23,9 | 25,2 |
Скориставшись оператором оцінювання 1МНК

дістанемо  = –1,081;
= –1,081; 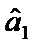 = 0,1178.
= 0,1178.
Економетрична модель має вигляд
 .
.
Коефіцієнт детермінації 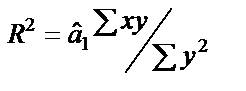 для цієї моделі
для цієї моделі  = 0,918, а це означає, що варіація заощаджень Y на 91,8% визначається варіацією доходів населення.
= 0,918, а це означає, що варіація заощаджень Y на 91,8% визначається варіацією доходів населення.
На перший погляд, результат наводить на думку, що специфікація моделі не містить помилки.
Але логічно висунути гіпотезу, що відхилення заощаджень від норми можуть бути пропорційними до доходу, тобто для цієї моделі дуже ймовірне існування гетероскедастичності залишків.
Отже, вихідну інформацію доцільно перетворити, поділивши обидві змінні на величину доходу X:

Таблиця
| Рік | |||||||||

| 0,041 | 0,022 | 0,008 | 0,019 | 0,009 | 0,010 | 0,032 | 0,037 | 0,030 |

| 0,114 | 0,106 | 0,100 | 0,094 | 0,091 | 0,084 | 0,079 | 0,074 | 0,070 |
| Рік | |||||||||

| 0,038 | 0,054 | 0,054 | 0,044 | 0,053 | 0,073 | 0,085 | 0,073 | 0,079 |

| 0,065 | 0,060 | 0,056 | 0,054 | 0,051 | 0,047 | 0,044 | 0,042 | 0,040 |
Нове рівняння зв’язку згідно з даними табл. має вигляд
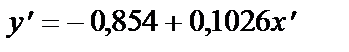 .
.
У результаті перетворення вихідних даних практично повністю змінилася специфікація моделі. Оскільки  , то цей зв’язок нелінійний. По-друге,
, то цей зв’язок нелінійний. По-друге,  характеризує відносний показник — рівень заощаджень, який припадає на одиницю доходу.
характеризує відносний показник — рівень заощаджень, який припадає на одиницю доходу.
Виконавши цю процедуру, дістанемо таке: спостереження з меншими значеннями 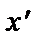 мають відносно більшу питому вагу при оцінюванні параметрів моделі, ніж у першому варіанті.
мають відносно більшу питому вагу при оцінюванні параметрів моделі, ніж у першому варіанті.
З наведеного прикладу бачимо, що явище гетероскедастичності не впливатиме на оцінки параметрів 1МНК, якщо певним чином перетворити вихідну інформацію. При цьому якщо економетрична модель має лише дві змінні, то це можна зробити так, як у прикладі.
Це перетворення, значно ускладнюється, якщо будується економетрична модель з багатьма змінними. У такому разі потрібно з’ясувати зміст гіпотези, згідно з якою  , де
, де  лишається невідомим параметром, а
лишається невідомим параметром, а 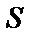 — відома симетрична додатно визначена матриця.
— відома симетрична додатно визначена матриця.
Поиск по сайту: