АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Параметричний тест Гольдфельда — Квандта

Читайте также:
  1. Внутрішня організація органу державної влади
  2. Для нижней группы
  3. Зразки тестових завдань
  4. Класифікація систем
  5. Методи обгрунтування управлінських рішень
  6. Методи та прийоми обґрунтування управлінських рішень
  7. На гетерокедастичность остатков
  8. Основні параметри бурових установок
  9. Прогноз.
  10. Тема: Гетероскедастичность
  11. Тема: Гетероскедастичность

Коли сукупність спостережень невелика, то розглянутий метод не застосовний.

У такому разі Гольдфельд і Квандт запропонували розглянути випадок, коли , тобто дисперсія залишків зростає пропорційно до квадрата однієї з незалежних змінних моделі:

Y = XA + u.

Для виявлення наявності гетероскедастичності згадані вчені склали параметричний тест, в якому потрібно виконати такі кроки.

Крок 1. Упорядкувати спостереження відповідно до величини елементів вектора Xj.

Крок 2. Відкинути c спостережень, які містяться в центрі вектора. Згід­но з експериментальними розрахунками автори знайшли оптимальні спів­відношення між параметрами c і n, де n — кількість елементів вектора :

Крок 3. Побудувати дві економетричні моделі на основі 1МНК за двома утвореними сукупностями спостережень 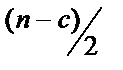за умови, що 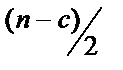перевищує кількість змінних m.

Крок 4. Знайти суму квадратів залишків за першою і другою моделями і :

, де 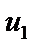— залишки за моделлю (1);

, де — залишки за моделлю (2).

Крок 7. Обчислити критерій

який в разі виконання гіпотези про гомоскедастичність відповідатиме F -роз­поділу з , ступенями свободи. Це означає, що обчислене значення R * порівнюється з табличним значенням F -крите­рію для ступенів свободи і і вибраного рівня довіри. Якщо 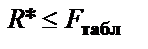, то гетероскедастичність відсутня.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)