Зразки тестових завдань

1. Математична модель –

А)система математичних співвідношень, яка описує об’єкт дослідження.

В)проект системи

С) Опис системи за допомогою математичних формул

2. Параметри моделі –

А) Y=(y₁,y₂, …,y_m).

В) А=(а₁,а₂, …,а_к).

С) Х=(х₁,х₂, …,х_n)

3. Величини Х, які описують зовнішні умови, та параметри моделі А визначають поза моделлю і називають

А) екзогенними (наперед відомими) змінними.

В) ендогенними змінними

С)генеральною сукупністю

4. Величини У, значення яких обчислюють за допомогою моделі, називають

А) екзогенними (наперед відомими) змінними.

В) генеральною сукупністю

С) ендогенними змінними

5. Моделі поділяють на теоретико-аналітичні (використовуються для дослідження загальних властивостей і закономірностей економіко-математичних процесів) та прикладні (використовуються для розв’язання конкретних економічних задач).

А) Залежно від об’єкта дослідження

В) Залежно від підходу до економічного дослідження й економічної практики

С) За призначенням

6. За способом відображення фактора часу моделі поділяються на

А) статичні (всі залежності відносяться до одного моменту часу) і динамічні(характеризують зміну економічних процесів в часі).

В) на лінійні і нелінійні

С) моделі виробництва, споживання, трудових ресурсів, ціноутворювання, фінансових рішень тощо

7. Залежність між двома змінними величинами хєХ та yєY назівають функціональною, якщо

А) зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).

В)кожному значенню незалежної змінної х відповідає одне значення залежної змінної у.

С) вплив зміни однієї не відображається на другій

8. Випадкові змінні х та у стохастично залежні, якщо

А) зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).

В)кожному значенню незалежної змінної х відповідає одне значення залежної змінної у.

С) вплив зміни однієї не відображається на другій

9. функція розподілу;диференціальна функція (щільність) розподілу – це

А) функціональні характеристики.

В) кількісні характеристики.

С)описові показники

10. Математичне сподівання,дисперсія,середнє квадратичне відхилення, моменти (початкові, центральні та ін.), мода,медіана- це

А) функціональні характеристики.

В) кількісні характеристики.

С)описові показники.

11. Вид зв’язку між двома випадковими змінними, при якому зміна значень однієї з них призводить до зміни середнього значення другої - це А) кореляційна залежність.

В) функціональна залежність

С) обернена залежність

12. При кореляційній залежності

А) кожному значенню факторної змінної х відповідає одне значення результуючої змінної у.

В)кожному значенню х відповідає постійне значення у.

С)кожному значенню факторної змінної х відповідає не одне, а кілька значень результуючої змінної у.

13. це рівняння

А)функціонального зв’язку

В) регресії

С)оберненої функції

14. Сукупність математичних методів, за допомогою яких досліджують взаємозв’язки кореляційно залежних змінних – це

А) функціональний аналіз

В) кореляційно-регресійний аналіз

С)графічний аналіз

15. Аналітичне групування –це

А) статистична таблиця

В) аналітичний вираз

С) графік

16. Сукупнісь математичних методів, за допомогою яких досліджуються і узагальнюються взаємозв’язки кореляційно зв’язаних змінних називається

А) математичним аналізом

В) кореляційно- регресійним аналізом

С) метод побудови моделі.

17. У лінійному рівнянні регресії

y =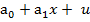

А) u – випадкова величина

В) u – коєфіцієнт кореляції

С) u - факторна змінна.

18. У лінійному рівнянні парної регресії кількість параметрів дорівнює

А) 3

В) 2

С) 1

19.Основним методо розв’язку лінійного рівняння регресії є

А) метод добутків

В) метод оберненої матриці

В) метод найменших квадратів

20. Метод, за яким знаходять найменше значення суми квадратів відхилень заданих значень результуючої змінної у_і від знайдених за рівнянням регресії теоретичних значень y ̃_i, називають

А) метод добутків

В) метод оберненої матриці

В) метод найменших квадратів

21.Коефіцієнт детермінації множинної регресії рахують за формулою:

А) ,

В) ;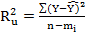

C) .

22. – це

А) дисперсія залишок;

В) коефіцієнт детермінації;

С) коефіцієнт кореляції.

23. – це

А) загальна дисперсія моделі;

В) коефіцієнт детермінації;

С) коефіцієнт кореляції.

24. Парні коефіцієнти кореляції дають оцінку тісноти зв'язку

А) між парами змінних;

В) між залишками;

С) між коефіцієнтами кореляції і детермінації.

25. Значимість зв'язку між залежною Y та залежними змінними X у випадку множинної регресії можна перевірити

А) за допомогою розподілу Ст’юдента;

В) за допомогою розподілу Фішера;

С) за допомогою розподілу Пірсона.

26. Якщо F>F_табл.

А) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії підтверджується;

В) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії відкидається;

С) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії потребує додаткового дослідження.

27. Якщо F<F_табл.

А) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії підтверджується;

В) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії відкидається;

С) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії потребує додаткового дослідження.

28. У кореляційному аналізі для характеристики відхилень коефіцієнта кореляції, як вибіркової величини, від свого "істотного" значення для перевірки використовується

А) t - критерій Ст'юдента;

В) F-критерія Фішера;

С) дисперсійний аналіз.

29. Матрицяі (X`X)^-1 – це

А) матриця залишків;

В) добуток обернених матриць;

С) матриця помилок.

30. Довірчі інтервали для параметра а_j встановлюються:

А) на підставі t-критерію і стандартної помилки;

В) на підставі F-критерію і стандартної помилки;

С) на підставі -критерію і стандартної помилки;

31. Існування тісної лінійної залежності, або кореляції, між двома чи більше пояснювальними змінними називається

А) автокореляція;

В) мультиколінеарність;

С) гомоскедастичність.

32.... негативно впливає на кількісні характеристики економетричної моделі або робить її побудову взагалі неможливою

А) автокореляція;

В) мультиколінеарність;

С) гомоскедастичність.

33. Основні наслідки мультиколінеарності:

А) Падає точність оцінювання;

В) коефіцієнт кореляції зростає;

С) коефіцієнт кореляції спадає.

34. Основні наслідки мультиколінеарності:

А) коефіцієнт кореляції зростає;

В) оцінки параметрів стають досить чутливими до обсягів сукупності спостережень

С) коефіцієнт кореляції спадає.

35. Коли серед парних коефіцієнтів кореляції пояснювальних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це означає можливість існування

А) автокореляції;

В) мультиколінеарності;

С) гомоскедастичності.

36.Мультиколінеарність означає існування

А) коефіцієнта кореляції;

В) зв’язку між змінними;

С) тісної лінійної залежності, або кореляції, між двома чи більше пояснювальними змінними.

37.Мультиколінеарність негативно впливає на

А)кількісні характеристики економетричної моделі;

В) кількість вибіркових даних;

С) критерій Фішера.

38. Коли між пояснювальними змінними існує функціональний зв’язок, то

А)оцінити вплив цих змінних на залежну взагалі неможливо;

В) для оцінки необхідні додаткові дані;

С) це не грає суттєвої ролі.

39. до основних наслідків мультиколінеарності відносяться:.

А) падає точність оцінювання;

В) оцінки параметрів деяких змінних моделі можуть бути незначущими через наявність їх взаємозв’язку з іншими змінними;

С) коефіцієнт кореляції стає від’ємним.

40. Коли серед парних коефіцієнтів кореляції пояснювальних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це означає можливість існування

А) гомоскедастичності;

В) мультиколінеарності;

С) гетероскедастичністі.

41. Коли коeфіцієнт частинної детермінації, який обчислено для регресійних залежностей між однією пояснювальною змінною та іншими, має значення, яке близьке до одиниці, то можна говорити про наявність

А) мультиколінеарності;

В) гомоскедастичності;

С) гетероскедастичністі.

42. За допомогою алгоритму Фаррара — Глобера досліджують

А) гомоскедастичность;

В) мультиколінеарность;

С) гетероскедастичність.

43. Методи перевірки гетероскедастичності для різних вихідних даних - це

А) алгоритму Фаррара — Глобера;

В) перевірка на основі критерію μ;

С) перевірка на основі критерію Фішера.

44. Параметричний тест Гольдфельда — Квандта застосовується для:

А) розрахунку коефіцієнта детермінації;

В) мультиколінеарності;

С) гетероскедастичністі.

45. Прогноз на перспективу буває:

А) точковий та інтервальний;

В) графічний;

С) прогноз створити не можна.

Зразки практичних завдань модуля