 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Приклад 9
Обчислити частинні коефіцієнти кореляції, скориставшись елементами матриці C:
Визначити t -критерій на основі частинних коефіцієнтів кореляції. Табличне значення t -критерію при 10-36 = 7 ступенях свободи і рівні значущості a = 0,05 дорівнює 1,69.
Зробити висновок, чи є всі пари незалежних змінних мультиколінеарними
Приклад 10
На базі 11 статистичнихданих певного регіону дослідити мультиколінеарність між факторами за допомогою алгоритму Фаррара — Глобера:
| № | Х1 | Х2 | Х3 | Х4 |
| 5,25 | 9,11 | 7,05 | 16,05 | |
| 11,24 | 13,57 | 8,68 | 18,68 | |
| 16,27 | 14,01 | 9,57 | 20,06 | |
| 18,75 | 17,29 | 10,10 | 29,67 | |
| 21,78 | 19,58 | 11,55 | 31,55 | |
| 24,58 | 21,07 | 13,31 | 34,01 | |
| 27,09 | 22,47 | 15,37 | 35,34 | |
| 31,76 | 24,68 | 17,01 | 36,01 | |
| 35,91 | 25,75 | 19,67 | 38,54 | |
| 38,57 | 27,05 | 21,92 | 41,92 | |
| 41,47 | 30,87 | 25,08 | 43,27 |
Зразок модульного завдання
ВАРІАНТ
Блок 1
1. 
це рівняння
А)функціонального зв’язку;
В) регресії;
С)оберненої функції.
2. Аналітичне групування –це
А) статистична таблиця;
В) аналітичний вираз;
С) графік.
3. 
– це
А) загальна дисперсія моделі;
В) коефіцієнт детермінації;
С) коефіцієнт кореляції.
4. Якщо F<Fтабл.
А) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії підтверджується;
В) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії відкидається;
С) гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії потребує додаткового дослідження.
5. Матрицяі (X`X)-1 – це
А) матриця залишків;
В) добуток обернених матриць;
С) матриця помилок.
6. Коли між пояснювальними змінними існує функціональний зв’язок, то
А)оцінити вплив цих змінних на залежну взагалі неможливо;
В) для оцінки необхідні додаткові дані;
С) це не грає суттєвої ролі.
7. Коли серед парних коефіцієнтів кореляції пояснювальних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це означає можливість існування
А) гомоскедастичності;
В) мультиколінеарності;
С) гетероскедастичністі.
8. Методи перевірки гетероскедастичності для різних вихідних даних - це
А) алгоритму Фаррара — Глобера;
В) перевірка на основі критерію μ;
С) перевірка на основі критерію Фішера.
9. Прогноз на перспективу буває:
А) точковий та інтервальний;
В) графічний;
С) прогноз створити не можна.
10. Величини Х, які описують зовнішні умови, та параметри моделі А визначають поза моделлю і називають
А) екзогенними (наперед відомими) змінними;
В) ендогенними змінними;
С)генеральною сукупністю.
Блок 2
1.Побудувати економетричну модель за даними таблиці. Оцінити параметри моделі. Зробити висновки.
| Номер сім’ї | 1 | 2 | 3 | 4 | 5 | 6 |
| Доход на 1 члена сім’ї, г.о. | 5,4 | 6,3 | 7,4 | 9,0 | 11,2 | 14,0 |
| Споживання молока в місяць, л | 8 | 10 | 11 | 13 | 15 | 17 |
2. Визначити значимість зв’язку між змінними Х та У за допомогою критерія Фішера.Перевірити значимість коефіцієнта кореляції за допомогою критерія Ст’юдента.
Значення Y та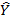 
взяти з таблиці:
| № | ||||||
| Y | 0.2 | 1.5 | 2.2 | |||
| 3.4 | 3.6 | 4.1 | 4.9 | 7.3 |
Матриця похибок має вигляд:
(X`X)-1 = 
.
3. Кореляційна матриця має вигляд:
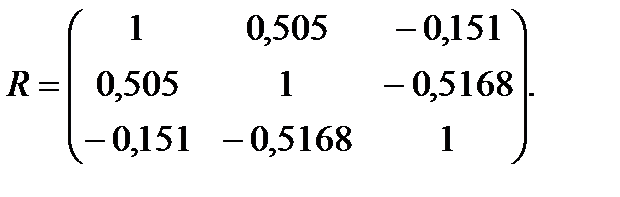
Якщо n=14, звернутися до алгоритму Фаррара — Глобера і оцінити незалежні змінні на мультиколінеарність з двома іншими за допомогою критерія Фішера (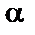
= 0,05).
Поиск по сайту: