АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Наслідки автокореляції залишків

Читайте также:
  1. Види та наслідки нерегульованої інфляції
  2. Відновлення репресій у 60-70-х рр. ХХ ст. Їх наслідки для розвитку культури.
  3. Глобалізація економіки: позитивні та негативні наслідки.
  4. Глобальні наслідки забруднення довкілля
  5. Економічні наслідки монополізму
  6. Економічні наслідки монополії
  7. Завершення промислової індустріалізації в Україні: соціально-економічна сутність та наслідки (1925-1939рр)
  8. ЗАВЕРШЕННЯ УКРАЇНСЬКОЇ НАЦІОНАЛЬНО-ДЕМОКРАТИЧНОЇ РЕВОЛЮЦІЇ, її НАСЛІДКИ ТА УРОКИ
  9. Зазначте причини виникнення, рушійні сили та наслідки Гайдамацького руху на Правобережжі у ХVІІІ ст.
  10. Зазначте причини та наслідки голоду 1946-1947 рр.
  11. Зазначте причини та наслідки ліквідації Гетьманщини.
  12. Зазначте причини, основні етапи та наслідки Національно-визвольної війни середини XVIІ ст.

Якщо знехтувати автокореляцією залишків і оцінити параметри моделі 1МНК, то дійдемо таких трьох наслідків.

1. Оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок 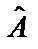можуть бути невиправдано великими.

2. Оскільки вибіркові дисперсії обчислюються не за уточненими формулами, то статистичні критерії t - і F -cтатистики, які знайдено для лінійної моделі, практично не можуть бути використані в дисперсійному аналізі.

3. Неефективність оцінок параметрів економетричної моделі призводить, як правило, до неефективних прогнозів, тобто прогнозів з дуже великою вибірковою дисперсією.

За відсутності автокореляції залишків матриця коваріацій для вектора оцінок 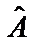така:

Припустимо, що незалежні змінні і залишки можна подати у вигляді стаціонарних марковських процесів першого порядку, тобто:

Якщо коефіцієнти l і r додатні, то говорять про додатну автокореляцію. Від’ємна автокореляція в економетричних моделях спостерігається дуже рідко.

Помилки 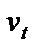і 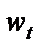взаємно незалежні і їх автокореляційні матриці діаго­нальні. Тоді можна показати, що звичайний метод найменших квадратів дає нам при достатньо великому n таку оцінку дисперсії параметрів :

.

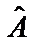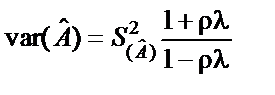Бачимо, що зміщення дисперсії параметрів тим більше, чим більші значення l і r (більша автокореляція). Нехай l= r = 0,5, тоді величина зміщення 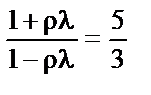. Цей множник і буде загубленим при використанні 1МНК, що призводить до заниження дисперсії порівняно з її справжнім значенням приблизно на 40%. При збільшенні l і r, наприклад, r = l = 0,8, зміщення буде 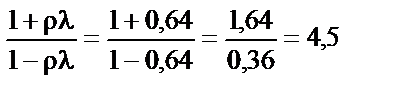, тобто істинне значення дисперсії у чотири з половиною рази перевищуватиме те, яке дістали при застосуванні 1МНК.

Якщо додатна автокореляція спостерігається і в залишках, і в незалежній змінній, то 1МНК дає зміщення і для залишкової дисперсії. Припустивши, як і раніше, що і підлягають однаковій схемі авторегресії, знайдемо:

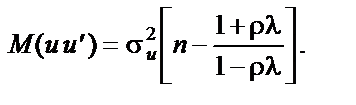
Якщо r = l = 0,5 і n = 20, то 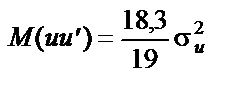, тобто недооцінка дисперсії залишків становить близько 4 %, а при r = l = 0,8; n = 20 ця недооцінка дорівнюватиме приблизно 20 %.

Отже, при застосуванні 1МНК вибіркові дисперсії будуть заниженими. Навіть після коригування оцінок вибіркових дисперсій на величину зміщен­ня не можна бути впевненим у коректності рівнів значущості для t - і F -cтатис­тик, оскільки наявність автокореляції залишків означає, що величина 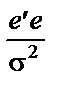може не розподілятися за законом c2 і не буде незалежною від .


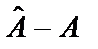1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)