Теореми додавання і множення

Сумою декількох подій називається подія, яка полягає в появі хоча б однієї з даних подій.

Добутком декількох подій називається подія, яка полягає в сумісному з’явленні усіх цих подій.

Різницею А – В двох подій А і В називається подія, яка полягає в тім, що подія А відбудеться, а подія В не відбудеться.

Теорема. Ймовірність суми несумісних подій дорівнює сумі ймовірностей цих подій:

(1.8)

Слідство 1. Сума ймовірностей подій, які утворюють повну групу, дорівнює одиниці:

(1.9)

Слідство 2. Сума ймовірностей протилежних подій дорівнює одиниці:

(1.10)

Приклад 1.7. В скриньці 20 червоних, 10 синіх і 5 білих ґудзиків. Знайти ймовірність витягнути з скриньки кольоровий ґудзик.

Розв’язання. Ймовірність взяти з скриньки червоний ґудзик дорівнює (подія А)

Ймовірність узяти з скриньки синій ґудзик дорівнює (подія В)

Події А і В несумісні (поява ґудзика одного кольору виключає появу ґудзика іншого кольору), тому можна застосувати теорему додавання несумісних подій.

Шукана ймовірність за формулою (1.8) дорівнює

.

Приклад1.8. В порт заходять судна тільки з трьох пунктів відправлення. Ймовірність появи судна з першого пункту дорівнює 0,2, з другого пункту – 0,6. Знайти ймовірність появи судна з третього пункту.

Розв’язання. Нехай подія А – в порт заходять судна з першого пункту, подія В

– в порт заходять судна з другого пункту, подія С – в порт заходять судна з третього пункту. Отже,

.

Тоді .

За умовою . Підставивши дані в формулу (1.9), отримаємо .

Дві події називаються незалежними, якщо поява однієї з них не змінює ймовірності появи іншої.

Декілька подій А, В,..., L називаються незалежними в сукупності (або просто незалежними), якщо незалежні любі дві з них і незалежна люба з даних подій і любі комбінації (добутки) подій, що залишилися. В протилежному випадку події А, В,..., L

називаються залежними.

Ймовірність події В за умови, що подія А вже відбулася, називається умовною ймовірністю і позначається або .

Теорема. Ймовірність сумісної появи двох залежних подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчислену в передбаченні, що перша подія відбулася

(1.11)

Теорема множення ймовірностей сумісної появи залежних подій легко узагальнюється на випадок довільного числа подій

, (1.12)

тт. ймовірність добутку декількох сумісних залежних подій дорівнює добутку ймовірності однієї з цих подій на умовні ймовірності інших, при цьому умовна ймовірність кожної послідуючої події обчислюється в передбаченні, що всі попередні події відбулися.

Приклад 1.9. В місті знаходиться 15 продовольчих і 5 непродовольчих крамниць. Навмання для приватизації були відібрані три крамниці. Знайти ймовірність того, що всі крамниці непродовольчі.

Розв’язання. Нехай подія А – першою відібрана для приватизації непродовольча крамниця; подія В – другою відібрана для приватизації непродовольча крамниця при умові, що подія А вже відбулася; подія С – третьою відібрана для приватизації непродовольча крамниця при умові, що події А і В вже відбулися.

Ймовірності подій А, В і С відповідно дорівнюють:

, , .

Застосувавши теорему множення декількох сумісних подій, тобто використавши формулу (1.12), матимемо

.

Теорема. Ймовірність сумісної появи двох незалежних подій дорівнює добутку ймовірностей цих подій:

(1.13)

Теорема множення ймовірностей сумісної появи декількох незалежних подій на випадок довільного числа подій

, (1.14)

тт. ймовірність добутку сумісної появи декількох незалежних подій дорівнює добутку ймовірностей цих подій.

Приклад 1.10. Ймовірність влучення в ціль для першого стрільця дорівнює 0,8, для другого – 0,7, для третього – 0,9. Кожний з стрільців зробив по одному пострілу. Яка ймовірність того, що в мішені три пробоїни.

Розв’язання. Позначимо події – влучення в ціль – го стрільця ();

В – в мішені три пробоїни. Тоді і події – незалежні. За теоремою множення незалежних подій і формулою (1.14), маємо

.

Теорема. Ймовірність появи хоча б однієї з подій незалежних в сукупності, дорівнює різниці між одиницею і добутком ймовірностей протилежних подій .

(1.15)

Якщо позначити , ,... , то формула (1.15) матиме вигляд

(1.16)

Слідство. Якщо події 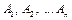мають однакову ймовірність, рівну 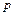, то ймовірність появи хоча б однієї з цих подій

(1.17)

Приклад 1.11. Ймовірність того, що при одному пострілі стрілець влучив в десятку дорівнює 0,6. Скільки пострілів повинен зробити стрілець, щоб з ймовірністю не менше 0,8 він влучив в десятку хоча б один раз?

Розв’язання. Позначимо через А – подію, що при 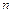пострілах стрілець влучить в десятку з ймовірністю 0,8 хоча б один раз. Події, що полягають у влученні в ціль при першому, другому пострілах і т.п. незалежні в сукупності, тому можливо застосувати формулу (1.17).

Прийнявши до уваги, що за умовою , отже , отримаємо:

, звідки .

Логарифмуючи цю нерівність за основою , отримаємо

.

Звідки, враховуючи, що , маємо

Отже, , тобто стрілець повинен зробити не менше 2 пострілів.

Приклад 1.12. Ймовірність того, що студент здасть перший іспит дорівнює 0,9; другий – 0,8; третій – 0,7. Знайти ймовірність того, що студентом будуть здані:

а) тільки 2 – й іспит; б) тільки один іспит; в) тільки два іспити; г) по крайній мірі два іспити; д) хоча б один іспит.

Розв’язання. а) Розглянемо події: – студент здасть – й іспит ;

В – студент здасть тільки другий іспит з трьох. Тоді подія , тт. сумісне здійснення трьох подій які полягають в тому, що студент здасть другий іспит і не здасть 1 – й і 3 – й іспити. Враховуючи, що події незалежні і за умовою

,

отримаємо

б) Нехай подія С – студент здасть один іспит з трьох. Подія С відбудеться, якщо студент здасть тільки перший іспит з трьох, або тільки другий, або тільки третій, тт.

+

в) Нехай подія – студент здасть тільки два іспити. Подія відбудеться, якщо здійсниться наступне: студент здасть перший і другий іспити і не здасть третього; здасть перший і третій іспити і не здасть другого; здасть другий і третій іспити і не здасть першого, тт.

= +

г) Нехай подія Е – студент здасть по меншій мірі два іспити (інакше: “хоча б два іспити” або “не менше двох” іспитів). Подія Е означає здачу любих двох іспитів з трьох або всіх трьох іспитів, тт. .

Отже,

д) Нехай подія К – студент здасть хоча б один іспит (інакше: “не менше одного” іспиту). Подія К являє собою суму подій С (три варіанта) і Е (чотири варіанта), тт.

(сім варіантів)

Проте простіше знайти ймовірність події К, якщо перейти до протилежної події, яка дає лише один варіант , тт. застосувати формулу (1.15). Отже,

.

Теорема. Ймовірність суми двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх добутку, тт.

(1.18)

Зауваження 1. Формула (1.18) має вигляд для незалежних подій

для залежних подій .

Зауваження 2. Якщо події А і В несумісні, то їх суміщення є неможлива подія і, отже . Формула (1.18) для несумісних подій прийме вигляд

.

Приклад 1.13. Знайти ймовірність того, що взяте навмання двохзначне число буде кратним 2 або 5 або тому і іншому одночасно.

Розв’язання. Нехай А – подія, яка відповідає тому, що двохзначне число кратне 2, а В – подія, яка відповідає кратності 5 двохзначного числа. Усього двохзначних чисел 90. Серед чисел, які кратні 2 буде 45, а кратних 5 – 18. Чисел, які кратні і 2 і 5 буде 9 (10; 20; 30; 40; 50; 60; 70; 80; 90). Отже, застосувавши теорему складання сумісних подій і враховуючи, що події А і В незалежні, за формулою (1.18), отримаємо

.

Поиск по сайту: