 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Генерация случайных чисел по различным законам распределения
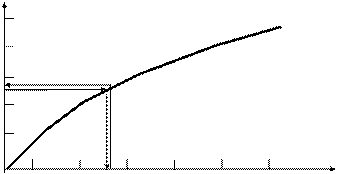
Генерация случайных чисел основана на том, что интегральная функция распределения F(x) ставит в соответствие любому заданному числу х вероятность от 0. до 1. Тогда наоборот некоторому значению F(x), равному, например r, соответствует определенная величина x (рисунок 2.14):
х = F-1(r),
где F-1 – функция, обратная F.
 |
1.0
F(x)
0.80
0.60 r
0.40
0.20
xr x
Рисунок 2.14 – Графическая интепретация получения случайных чисел по заданному закону распределения
Отсюда следует способ формирования случайных чисел с заданным законом распределения, называемый методом обратных функций. Метод реализуется как по функциональным, так и аппроксимирующим зависимостям. При этом значения r должны быть распределены в интервале 0. – 1. случайно по равномерному закону.
Для нормального закона распределения применяется также метод, основанный на центральной предельной теореме теории вероятностей, согласно которой большое число n независимых случайных чисел с одним и тем же распределением вероятностей дает нормально распределенные числа с математическим ожиданием, равным сумме этих чисел и геометрической суммой среднеквадратических отклонений:
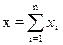 ;
;  .
.
Формулы для получения случайных чисел по некоторым законам распределения приведены в таблице 2.1.
Псевдослучайные равномерно распределенные числа в интервале 0. – 1.0 можно получать по специальным алгоритмам или применить стандартные функции и подпрограммы языков программирования – RND (Basic), RANDOM (Pascal), RAN, RANDU (Fortran – функция и подпрограмма). Генерируемая последовательность может задаваться с помощью оператора, например RANDOMIZE.
Таблица 2.1 – Получение случайных чисел
| Закон рас-пределения | Получение случайных чисел для базового закона | Получение случайных чисел для усеченных (xн<x<xв) или сдвинутых распределений (x>xc) |
| Равномер-ной плотности | 
 ; ; 
| – |
| Нормальный |  а = xм; s =S
а = xм; s =S
| Для усеченного по выражению для базового, если полученное xн<x<xв, иначе попытка повторяется |
| Логарифми-чески нормальный |   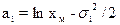
| Для сдвинутого   
|
| Экспонен-циальный | 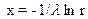 l= 1/xм
l= 1/xм
| Для сдвинутого
 lс= 1/(xм -xc)
lс= 1/(xм -xc)
|
| Релея | 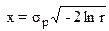

| Для сдвинутого


|
| Вейбулла | 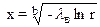
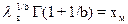 ; ;

| Для сдвинутого

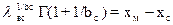 ; ;

|
| Эрланга | 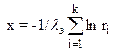
 , k=1, 2, 3,...; , k=1, 2, 3,...;

| Для сдвинутого

 , kc=1, 2, 3,...; , kc=1, 2, 3,...;
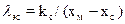
|
Наиболее распространенными способами получения псевдослучайных равномерно распределенных чисел в интервале 0.  – 1.0 являются:
– 1.0 являются:
мультипликативный;
смешанный;
с использованием числа p;
с использованием тригонометрических функций.
Алгоритм смешанного метода следующий:
 1-й вход
1-й вход
 |
r = rн 0.0 < rн < 1.0
p = pн pн = 8. I ±3, I = 2,3,...
 |
 Последу-
Последу-
r = r p  +a- int(r p
+a- int(r p  +a)
+a)
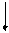 ющие
ющие
входы выход
Наиболее часто в качестве a принимается число пи (a=p).
Мультипликативный метод отличается от смешанного тем, что a=0. В этом случае начальное значение rн ≠0,5.
При большом числе сгенерированных случайных чисел оценка их математического ожидания должна стремится к 0.5 и среднеквадратическое отклонение к  .
.
Пример. Получить зависимость для генерации случайных чисел по экспоненциальному закону распределения.
Интегральная функция экспоненциального распределения имеет вид
 , x ³ 0
, x ³ 0
где l – параметр распределения (l = 1/ xм , xм – оценка математического ожидания случайной величины).
Для получения случайного числа x по r приравняем выражение для F(x) и величину r и выразим x:
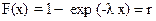 ;
;
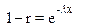 ;
;
 ;
;
 .
.
Поиск по сайту: