 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Исследование статистических зависимостей между случайными величинами
При решении многих задач, в том числе и оптимизационных, возникает необходимость в нахождении модели связи зависимой переменной от различных факторов (например, расход топлива автомобилем от его полной массы, скорости движения, суммарного дорожного сопротивления, температуры воздуха и других факторов). Такие зависимости называются уравнениями множественной регрессии (функциями отклика). Они описывают статистические зависимости между параметрами систем и процессов и могут быть использованы для обоснования нормативов, отыскания оптимальных решений и прогнозирования развития явлений.
Чтобы математические модели связи отражали объективные закономерности исследуемых процессов и явлений, они должны учитывать их физическую сущность, а также влияние внешних и внутренних факторов. Для этого планируются и проводятся эксперименты и обрабатывается полученная информация.
В общем виде уравнение регрессии имеет вид
yт = f(x1,x2,...,xn),
где yт – зависимый параметр;
x1,x2,...,xn – факторы (аргументы), представляющие собой учитываемые (управляемые) переменные, значения которых фиксируются в ходе эксперимента;
n – число учитываемых факторов.
Уравнение регрессии может иметь аддитивный (*) или мультипликативный (**) вид
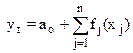 ; (*)
; (*)
 . (**)
. (**)
В качестве функций f(x) наиболее часто применяются следующие:
y = a x + b;
y = a / x + b;
y = x / (a x + b);
y = 1 / (a x + b);
y = a x2 + b x + c;
y = a xc + b;
y = a ln(x) + b;
y = a ln(x) + b x +c;
y = b ax;
y = b x a;
y = b a(1/x);
y = 1 / (a exp (-x) + b);
y = exp (a x + b).
При множественной регрессии широко применяются аддитивная линейная

или мультипликативная степенная модель
 .
.
Компьютерная программа нахождения парных зависимостей между случайными величинами приведена в приложении 3.
Эксперимент может быть активным и пассивным. При пассивном эксперименте фиксируют складывающиеся при протекании реальных процессов значения факторов и зависимой переменной. Активный эксперимент проводится по заранее составленному плану.
При активном эксперименте факторы фиксируются на определенных уровнях (при определенных значениях). Совокупность уровней факторов называют факторным пространством или решеткой планирования. Записанные значения (уровни) факторов в таблицу называют матрицей планирования. Каждой точке факторного пространства соответствует экспериментальное значение зависимой переменной.
Активный эксперимент может быть полнофакторным и дробнофакторным. При полнофакторном эксперименте рассматриваются все возможные сочетания различных уровней факторов. Число точек (m) решетки планирования полнофакторного эксперимента составляет
m = k n,
где к – число уровней, на которых зафиксирован каждый фактор; n – число факторов.
Например, при k=3 и n=2 получаем m=9 с планом испытаний по нижеследующей схеме
(-1, 0 и +1 - соответственно нижний, средний и верхний уровни значений факторов):
| -1,+1 | 0,+1 | +1,+1 |
| -1,0 | 0,0 | +1,0 |
| -1,-1 | 0,-1 | +1,-1 |
При k=3 и n=3 получаем нижеприведенный план эксперимента (-, 0 и + соответственно нижний, средний и верхний уровни значений факторов):
| Факторы | + | + | + | + | + | + | + | + | + | - | - | - | - | - | - | - | - | - | ||||||||||
| - | - | - | + | + | + | - | - | - | + | + | + | - | - | - | + | + | + | |||||||||||
| - | + | - | + | - | + | - | + | - | + | - | + | - | + | - | + | - | + |
Дробнофакторный эксперимент предусматривает проведение опытов в определенных точках, назначенных по специальным алгоритмам. В этом случае число опытов меньше чем при полнофакторном эксперименте. Примером дробнофакторного эксперимента является "латинский" квадрат, у которого по строкам и столбцам значения уровней факторов не повторяются. Для k=3 и n=3 в этом случае план эксперимента следующий:
+ -0
0 + -
- 0 +
При проведении пассивного эксперимента необходимо также фиксировать такие наборы значений факторов, которые как можно более полно охватывают исследуемое факторное пространство.
Для определения уравнения регрессии число опытов m должно быть не менее числа оцениваемых его параметров.
Нахождение параметров уравнения регрессии (функции отклика) производится по методу наименьших квадратов:
 ,
,
где m – число зафиксированных значений зависимой переменной;
yэi – экспериментальные значения зависимой переменной при i-м опыте;
yтi – теоретические (выравненные) значения зависимой переменной при i-м опыте;
 – j-й параметр уравнения регрессии.
– j-й параметр уравнения регрессии.
Взяв, частные производные по искомым параметрам и приравняв их нулю, получаем систему из n уравнений по числу неизвестных. Решение полученной системы дает значения параметров уравнения регрессии.
Например, для зависимости y=ax+b получаем:
 .
.
Берем частные производные по искомым параметрам a и b:
 ;
;
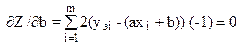 .
.
После упрощений получаем систему:



из которой выражаются неизвестные параметры a и b:
 ;
;
 .
.
Изучение статистических зависимостей основывается на корреляционно-регрессионном анализе. Корреляционный анализ позволяет ответить на вопрос о существовании зависимости между случайными величинами, а также оценить степень тесноты статистической зависимости. Инструментом регрессионного анализа является уравнение регрессии. Исходными данными для проведения корреляционно-регрессионного анализа является статистическая информация, содержащая значения факторов и зависимого от них параметра.
Одной из возможных схем проведения корреляционно-регрессионного анализа является следующая:
1) проводится взаимный парный корреляционный анализ между всеми возможными сочетаниями факторов и при существенности связи между факторами пары один из дублирующих друг друга факторов (зависимый фактор) исключается из дальнейших расчетов;
2) принимается вид уравнения регрессии (модели связи);
3) рассчитываются параметры уравнения регрессии;
4) проверяется значимость отдельных факторов в модели и адекватность уравнения регрессии экспериментальным данным в целом. Если нет малозначимых факторов и уравнение регрессии согласуется с экспериментальными данными – исследование закончено, а иначе на п.5;
5) при наличии малозначимых факторов они исключаются из расчетов и переход на п. 3 и при неадекватности уравнения регрессии экспериментальным данным переход на п. 2 для принятия нового вида уравнения регрессии.
Если связь оказалась несущественной для различных видов уравнения регрессии, то необходимо считать, что зависимая переменная не зависит от учитываемых факторов.
Полученное уравнение регрессии является моделью связи между факторным пространством и зависимой переменной (параметром).
Статистикой, характеризующей тесноту связи между факторами и зависимой переменной, является коэффициент множественной корреляции.
Коэффициент множественной корреляции показывает, какая часть дисперсии зависимой переменной объясняется полученным уравнением регрессии
 ,
,
где  – объясненная сумма квадратов отклонений от оценки математического ожидания;
– объясненная сумма квадратов отклонений от оценки математического ожидания;
 – полная сумма квадратов отклонений от оценки математического ожидания;
– полная сумма квадратов отклонений от оценки математического ожидания;
yм – оценка математического ожидания случайной величины.
Разность между полной и объясненной суммой квадратов является остаточной (необъясненной) суммой отклонений от оценки математического ожидания
 .
.
Тогда через  значение коэффициента множественной корреляции рассчитывается по формуле
значение коэффициента множественной корреляции рассчитывается по формуле
 .
.
Значения R может быть в пределах от 0 до 1.0. При R = 0 связь между факторами и зависимой переменной отсутствует, а R = 1.0 указывает на функциональную зависимость.
Значимость факторов оценивается по критерию Стьюдента.
Статистика критерия Стьюдента tj рассчитывается по формуле
tj = abs(aj / saj),
где bj – значение j-го параметра (коэффициента) в уравнении регрессии;
s bj – среднеквадратическое отклонение параметра bj.
Если расчетное значение статистики критерия Стьюдента tj для выборочного параметра (коэффициента) при рассматриваемом факторе больше табличного значения критерия tт γ,k, то считается, что нет оснований считать данный фактор малозначимым. Табличное значение tтγ,k определяется заданной доверительной вероятностью γ и числом степеней свободы k. Число степеней свободы определяется по выражению
k = m - n - 1,
где m – число эмпирических точек, в которых определен зависимый параметр; n – число факторов, входящих в уравнение регрессии.
Доверительный уровень значимости рекомендуется принимать равным 0.01–0.1 (чем меньше γ, тем выше требования к значимости фактора).
Для проверки существенности коэффициента множественной корреляции и таким образом оценивания согласованности уравнения регрессии с экспериментальными данными используется статистика критерия Фишера
 или
или
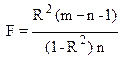 ,
,
где  и
и  – соответственно объясненная и остаточная дисперсия для зависимого параметра.
– соответственно объясненная и остаточная дисперсия для зависимого параметра.
Чтобы не было оснований отвергнуть гипотезу, что экспериментальные данные согласуются с полученным уравнением регрессии, рассчитанная статистика критерия Фишера должна быть больше табличного значения (F > Fт). Табличное значение Fт определяется в зависимости от уровня значимости γ и числа степеней свободы k1 и k2:
k1 = n;
k2= m - n- 1.
Уровень значимости (вероятность) рекомендуется принимать 0.01 – 0.05 (чем меньше, тем жестче требования к адекватности модели).
Если F<Fт, то считается, что уравнение регрессии не согласуется с экспериментальными данными.
Статистику критерия Фишера можно использовать для оценки значимости отдельных факторов. Фактор следует считать малозначимым в том случае, если его исключение из модели не вызывает существенного снижения статистики критерия Фишера. При этом исключение малозначимого фактора может обеспечить увеличение статистики F. Например, если при m=7 и n=3 имели  =2.1, а
=2.1, а  =0.7, а при исключении одного из факторов (n=2) получили
=0.7, а при исключении одного из факторов (n=2) получили  =1.8 и
=1.8 и  =1.0, то
=1.0, то
 =3.0 при n=3;
=3.0 при n=3;
 =3,6 при n=2.
=3,6 при n=2.
Увеличение статистики F в приведенном примере указывает на малозначимость исключаемого из модели фактора.
Мерой согласованности уравнения регрессии с экспериментальными данными может служить также коэффициент средней линейной ошибки аппроксимации E
 .
.
Компьютерная программа проведения множественного корреляционно-регресионного анализа приведена в приложении 4.
Поиск по сайту: