 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Отыскание кратчайших расстояний и путей между пунктами транспортной сети. Кратчайшая связывающая сеть
Транспортная сеть района (региона) представляет собой систему путей сообщения, предназначенную для передвижения транспортных средств. Модель транспортной сети – это описание местонахождения ее вершин (пунктов), а также длин и других параметров (характеристик) соединяющих вершины звеньев. Может быть задана в графическом или табличном виде. Звеном транспортной сети является ее часть, соединяющая две смежные вершины. Длина звеньев может быть выражена в единицах длины, приведенных единицах длины, единицах времени и стоимостном выражении (в дальнейшем длина). В качестве других параметров звеньев может быть задана техническая категория пути сообщения и др. Вершины (пункты) транспортной сети соответствуют местонахождению ресурсообразующих и ресурсопоглащающих точек, терминалов, пересечений путей.
Длина звеньев транспортной сети определяется по справочным таблицам, атласам дорог, с помощью курвиметра по масштабным картам и планам, а также непосредственным замером на местности, например по показаниям одометра (счетчика пройденного пути) автомобиля.
Отыскание кратчайших расстояний между пунктами транспортной сети возможно по методу потенциалов, методу "метлы", динамическому методу, на основе теории графов (метод Флойда) и др.
Например, задача отыскания кратчайших расстояний между пунктами транспортной сети методом потенциалов решается по следующему алгоритму:
1) Начальному пункту, от которого требуется определить кратчайшие расстояния, присваивается потенциал vi = 0.
2) Находятся все звенья, для которых начальным пунктам i присвоены потенциалы vi, а конечным пунктам j не присвоены. Если таких звеньев нет, то решение закончено (на п.5), а иначе на следующий п.3.
3) Для найденных звеньев по п.2 рассчитываются значения потенциалов конечных пунктов j по следующей формуле:
uj(i) = vi + lij,
где uj(i) – потенциал конечного пункта j звена i-j; lij – длина звена i-j.
Из всех полученных потенциалов выбирается потенциал с наименьшим значением, т.е. определяется:
 ,
,
где { uj(i) } – множество значений потенциалов конечных пунктов j звеньев i-j, i-м начальным пунктам которых ранее присвоены потенциалы; ur(s) – потенциал конечного пункта r звена s-r, являющийся наименьшим по значению элементом множества { uj(i) }.
Потенциал ur(s) присваивается соответствующему конечному пункту (vs = ur(s)), а звено r-s отмечается стрелкой.
В случае если несколько значений потенциалов множества {vj(i)} окажутся равными и наименьшими, то необходимо установить, относятся они к одному и тому же пункту или нет.
Если наименьшие равные значения потенциалов относятся к различным пунктам (у потенциалов не совпадают цифровые индексы без скобок), эти значения потенциалов присваиваются всем соответствующим конечным пунктам и стрелками отмечаются соответствующие звенья.
Если наименьшие равные значения потенциалов относятся к одному и тому же конечному пункту r (у потенциалов совпадают цифровые индексы без скобок), то пункту r присваивается это наименьшее значение потенциала и отмечается стрелкой то звено s-r, которому соответствует потенциал ur(s) с большим удельным весом в его составе длин звеньев с лучшими условиями перемещения. При одинаковых дорожных условиях кратчайшее расстояние в этом случае реализуется по одному (любому) из звеньев s-r.
4) переход на п. 2
5) формируется окончательное решение. Величина потенциалов у вершин показывает кратчайшие расстояния от выбранного начального пункта до каждой вершины, а звенья с входящими друг в друга стрелками образуют кратчайший путь движения от интересующего пункта до исходного. Если два пункта сети соединены таким путем, то кратчайшее расстояние между ними равно разности их потенциалов.
Принимая за начальный последовательно каждый из пунктов сети и выполняя действия по вышеописанному методу, получают таблицу кратчайших расстояний между всеми пунктами транспортной сети (таблица 3.2). Кратчайшие расстояния необходимо знать для оптимизации грузопотоков, маршрутизации перевозок, закрепления маршрутов за перевозчиками и т.п.
Таблица 3.2 – Кратчайшие расстояния между пунктами транспортной сети (км)
| Пункты | ... | j | ... | n | |||
| l1j | l1n | ||||||
| . . . | |||||||
| i | li1 | lij | lin | ||||
| . . . | |||||||
| n | ln1 | lnj | lnn=0 | ||||
Пример. Необходимо найти кратчайшие расстояния от пункта 1 до остальных пунктов нижеприведенной транспортной сети (рисунок 3.20).
 |
2 5
6км
5км 6 км
3 11
3 км
0 1 4 11
5 км
6 км
5 6
Рисунок 3.20 – Схема транспортной сети
Решение.
Шаг 1. Начальному пункту 1 присваивается потенциал v1 = 0 (потенциалы указаны в квадратах).
Шаг 2.
1-й этап. Звенья, начальным пунктам i которых присвоен потенциал vi, а для конечных пунктов j потенциалы не присвоены: 1-2 и 1-5. Рассчитываются значения потенциалов конечных пунктов j:
u2(1) = v1 + l1-2 =0+5=5
u5(1) = v1 + l1-5 =0+6=6
Из рассматриваемых на данном этапе потенциалов находится минимальный
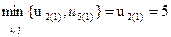 .
.
Потенциал u2(1) присваивается соответствующему конечному пункту (v2 = u2(1) =5), а звено 1-2 отмечается стрелкой.
2-й этап. Звенья, начальным пунктам i которых присвоен потенциал vi, а для конечных пунктов j потенциалы не присвоены: 1-5, 2-3 и 2-4. Рассчитываются значения потенциалов конечных пунктов j:
u5(1) = v1 + l1-5 =0+6=6
u3(2) = v2 + l2-3 =5+6=11
u4(2) = v2 + l2-4 =5+6=11
Из рассматриваемых на данном этапе потенциалов находится минимальный
 .
.
Потенциал u5(1) присваивается соответствующему конечному пункту (v5 = u5(1)), а звено 1-5 отмечается стрелкой.
3-й этап. Звенья, начальным пунктам i которых присвоен потенциал vi, а для конечных пунктов j потенциалы не присвоены:, 2-3, 2-4 и 5-4. Рассчитываются значения потенциалов конечных пунктов j:
u3(2) = v2 + l2-3 =5+6=11
u4(2) = v2 + l2-4 =5+6=11
u4(5) = v4 + l5-4 =6+5=11
Из рассматриваемых на данном этапе потенциалов находится минимальный
 .
.
Минимальное значение потенциалов, равное 11, присваивается соответствующим конечным пунктам v3=11 и v4 =11 (первый частный случай), и звено 2-3, а также, например, 2-4 (одно из двух 2-4 и 5-4 – второй частный случай) отмечаются стрелкой.
4-й этап. Так как потенциалы присвоены всем пунктам, то решение закончено.
Алгоритм метода отыскания кратчайших расстояний, который легко реализуется на компьютере, и поясняющая схема приведены на рисунке 3.21. Реализация данного алгоритма в виде компьютерной программы приведено в приложении 7.
Кратчайшая связывающая сеть (КСС) представляет собой "дерево" графа минимальной длины, т.е. она не должна содержать контуров (циклов) и включать звенья, которые дают суммарную минимальную длину. Применяется для нахождения сети маршрутов минимальной длины, соединяющей заданные пункты (маршруты перевозок пассажиров или мелких партий грузов, сеть путей с определенными свойствами и т.п.).
Один из алгоритмов отыскания кратчайшей связывающей сети следующий:
1) находится звено минимальной длины и включается в КСС;
2) последовательно включаются звенья в КСС:
2.1) находятся звенья, соединенные только одним своим концом с имеющейся частью КСС. Если нет ни одного такого звена, то решение закончено. Иначе переход на следующий пункт 2.2;
2.2) из найденных по п. 2.1 звеньев определяется звено минимальной длины и включается в КСС;
2.3) переход на 2.1.
Кратчайшая связывающая сеть включает ровно m-1 звеньев при числе вершин m.
Пример. Необходимо найти кратчайшую связывающую сеть для ранее приведенной схемы транспортной сети.
Решение.
1) находим из всех звеньев звено минимальной длины и включаем в КСС сеть (звено 3-4);
2) последовательно включаем звенья в КСС:
1-итерация
2.1.1) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Это звенья 3-2, 4-2 и 4-5.
2.2.1) из выбранных звеньев находим звено минимальной длины и включаем в КСС. Это звено 4-5;
2.3.1) переход на 2.1.2.
2- итерация
2.1.2) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Это звенья 3-2, 4-2 и 5-1.
2.2.2) из выбранных звеньев находим звено минимальной длины и включаем в КСС. Поскольку все звенья равной минимальной длины, то выбираем любое из них, например звено 5 - 1;
2.3.2) переход на 2.1.3.
3- итерация
2.1.3) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Это звенья 3-2, 4-2 и 1-2.
2.2.3) из выбранных звеньев находим звено минимальной длины и включаем в КСС. Это звено 1-2;
переход на 2.1.4.
4- итерация
2.1.4) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Таких звеньев нет. Решение закончено.
Звенья КСС выделены линиями большей толщины (рисунок 3.22).
 Пуск
Пуск
2
Ввод n, ip n – число вершин транспортной сети
ip – признак одностороннего движения (0 – нет, 1 – да);
3 5
ip=1 Нет Ввод sij, sij –длина звеньев (вводится
 ;
;  1Е20, если звена нет)
1Е20, если звена нет)
Да
4 6
sij, sji =sji,
 ;
; 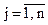 ,i¹j
,i¹j  ;
; 
sij=0, i = j
8 16 sij –расстояние между пунктами i и j
 Вывод s i j, p i j pij – промежуточный пункт на пути
Вывод s i j, p i j pij – промежуточный пункт на пути
 ;
; 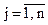 между i и j
между i и j
9 17
 Останов
Останов
10 Да Sjk k
sj i > 1E19 Sik
j Sji i
Нет

Да 12 Нет 13
s i k > 1E19 c = s ji + s i k
15 Да 14
s j k = c c < s jk
p j k = i
Нет Рисунок 3.21 – Алгоритм метода поиска
кратчайших расстояний между пунктами транспортной сети
 2
2
6км
5км 6 км
3 км
1 4
5 км
6 км
Рисунок 3.22 – Схема кратчайшей связывающей сети (жирные линии)
Поиск по сайту: