Целочисленная задача линейного программирования

Задача состоит в следующем:

необходимо найти оптимальные значения управляемых параметров { K_i }, дающие экстремум целевой функции

при ограничениях

, ; ;

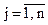K_i = 0,1,2,...,

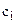– эффект от одной единицы K_i; K_i – значение i-го оптимизируемого параметра; a_ij и b_j – параметры ограничений; m – общее число оптимизируемых параметров; n – общее число ограничений.

Решение задачи без учета целочисленности с последующим округлением, отбрасыванием дробной части и т.п. не дает правильного ответа.

Например, для нижеприведенной задачи (рисунок 3.27), как следует из ее графического решения, нецелочисленное решение в точке А (K₁ = 1.6, K₂ = 2.6). При округлении K₁=2, K₂=3 нарушается заданное ограничение, при отбрасывании дробной части K₁ = 1, K₂ = 2 не гарантировано оптимальное решение. Если провести линию дополнительного ограничения, которое не отсекает ни одного целочисленного решения, то очевидно, что максимум Z достигается в точке K₁ =3, K₂=0.

Решение задачи производится по следующему алгоритму:

1) решается задача линейного программирования (ЗЛП) без учета целочисленности оптимизируемых параметров;

2) полученное решение проверяется на целочисленность. Если целочисленно, то решение получено (ВЫХОД), иначе на п. 3;

3) строится дополнительное ограничение, отсекающее часть области допускаемых нецелочисленных значений;

4) решается ЗЛП с дополнительным ограничением;

5) возврат к п.2.

Формирование дополнительных ограничений осуществляется по алгоритму Гомори, называемым правильным отсечением. Отсекающая плоскость должна быть линейной и исключать найденное оптимальное нецелочисленное решение и не отсекать ни одной из допускаемых целочисленных точек /17/.

К₂ изолиния целевой функции

4

3 2-е ограничение

дополнительное

А ограничение

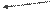1-е ограничение

1 2 3 4 К₁

Рисунок 3.27 – Пример графического решения целочисленной задачи линейного программирования

Поиск по сайту: