 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение. Проверяем задачу на сбалансированность, для чего рассчитываем суммарный объем наличия ресурса XсА и суммарный объем потребности в ресурсе XсВ
Проверяем задачу на сбалансированность, для чего рассчитываем суммарный объем наличия ресурса XсА и суммарный объем потребности в ресурсе XсВ
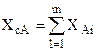 = 15+30+40=80;
= 15+30+40=80; 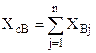 = 10+10+20+30=70.
= 10+10+20+30=70.
После этого сравниваем объемы XсА и XсВ. Поскольку они не равны, то задача несбалансирована. Так как XсА >XсВ, то вводится фиктивный потребитель В5 (n=n+1) и по не нему назначается объем ресурса в размере XВ5 = abs(XсА - XсВ)=80-70=10. Для фиктивного потребителя назначаются стоимости (расстояния) равными постоянной величине, например, lф= 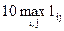 = 8*10=80(li5 = 80, i=1,2,3). Однако в связи с тем, что транспортные средства 2-го предприятия необходимо использовать в полном объеме, то расстояние l2-5 следует принять значительно больше других, например, l2-5=800. Затем по фиктивному пункту назначаются ограничения равными постоянной величине, например, Xoф³ abs(XсА - XсВ) ³ 10 (для фиктивного потребителя Xoi5 = 10, i=1,2,3).
= 8*10=80(li5 = 80, i=1,2,3). Однако в связи с тем, что транспортные средства 2-го предприятия необходимо использовать в полном объеме, то расстояние l2-5 следует принять значительно больше других, например, l2-5=800. Затем по фиктивному пункту назначаются ограничения равными постоянной величине, например, Xoф³ abs(XсА - XсВ) ³ 10 (для фиктивного потребителя Xoi5 = 10, i=1,2,3).
Для учета запрещения поставки ресурса от поставщика А1 потребителю В4 заменяем реальную стоимость (расстояние) l1-4 на большое число, например  . Принимаем l1-4=80.
. Принимаем l1-4=80.
Обеспечение поставки от поставщика А2 потребителю В2 в гарантированном объеме Xг2-2=5 производится следующим образом:
в окончательное решение вводится корреспонденция X2-2 = 5;
корректируются соответствующие размеры наличия и потребности в ресурсе
XА2 =XА2 - X2-2 =30-5=25; XB2 = XB2 - X2-2 =10-5=5.
С учетом исходных условий и последующих изменений составляем распределительную таблицу (таблица 3.5) и производим первоначальное базисное распределение по методу минимального элемента. Для этого назначаем корреспонденции для связей в порядке возрастания по ним стоимостей (расстояний). Связи загружаются в следующей последовательности: А1-В3 объемом 10, А3-В2 объемом 5, А3-В3 объемом 10; А3-В4 объемом 25, А2-В1 объемом 10, А2-В4 объемом 5, А2-В5 объемом 10.
Полученное первоначальное распределение проверяем на оптимальность, для чего рассчитываем значения потенциалов uAi и uBj. При этом значение одного из потенциалов, например для А1, задаем равным нулю (uA1 =0). После того, как определены значения потенциалов, для каждой свободной связи рассчитываем оценочный параметр sij по формуле (3.6).
Таблица 3.5 – Распределительная таблица (первоначальное базисное распределение)
| Поставщики Ai | Потребители Bj | X Ai | uAi | |||||||
| B1 | B2 | B3 | B4 | B5 | ||||||
| A1 | +3 4 | +6 8 | +77 80 | -716 80 | ||||||
| A2 | -2 4 | -2 4 |
+ 5
| 10 – | ||||||
| A3 | +3 5 | – 25 | -717 80 + | |||||||
| X Bj | ||||||||||
| uBj |
Если для свободной связи sij ³0, то связь не является потенциальной, sij<0 – потенциальна. В первоначальном распределении потенциальными оказались связи A1-B5, A3-B5, A2-B2 и A2-B3 соответственно с оценочными параметрами, равными (-716), (-717), (-2) и (-2).
Для связи A3-B5, как для наиболее потенциальной, строится контур, и по нему перераспределяются корреспонденции с загрузкой потенциальной связи. Связи A2-B4 и A3-B5 (связи со знаком +) догружаются объемом по 10 ед. (минимальный для связей со знаком -), а для связей A2-B5 и A3-B4 (связи со знаком -) снимается объем по 10 ед. В результате получаем улучшенный план закрепления маршрутов за предприятиями (1-е улучшенное базисное распределение) (таблица 3.6).
Таблица 3.6 – Распределительная таблица (1-е улучшенное базисное распределение)
| Поставщики Ai | Потребители Bj | X Ai | uAi | ||||
| B1 | B2 | B3 | B4 | B5 | |||
| A1 | +3 4 | +6 8 | +77 80 | +1 80 | |||
| A2 | -2 4 + | -2 4 | – 15 | 717 800 | |||
| A3 | +3 5 | – 5 | + 15 | ||||
| X Bj | |||||||
| uBj |
В улучшенном распределении потенциальными оказались связи A2-B2 и A2-B3 соответственно с оценочными параметрами, равными (-2) и (-2).
Для связи A2-B2, как одной из наиболее потенциальных, строится контур, и по нему перераспределяются корреспонденции с загрузкой потенциальной связи. Связи A2-B2 и A3-B4 (связи со знаком +) догружаются объемом по 5 ед. (минимальный для связей со знаком -), а для связей A3-B2 и A2-B4 (связи со знаком -) снимается объем по 5 ед. В результате получаем 2-е улучшенное базисное распределение (таблица 3.7).
Таблица 3.7 – Распределительная таблица (2-е улучшенное базисное распределение)
| Поставщи- Ки Ai | Потребители Bj | X Ai | uAi | ||||
| B1 | B2 | B3 | B4 | B5 | |||
| A1 | +3 4 | +8 8 | +77 80 | +1 80 | |||
| A2 | -2 4 | -2 4
 + +
| – 10 | 717 800 | |||
| A3 | +3 5 | – 3 | + 4 | ||||
| X Bj | |||||||
| uBj |
Производим проверку полученного распределения на оптимальность.
В улучшенном распределении потенциальной оказалась связь A2-B3 с оценочным параметром, равным (-2).
Для связи A2-B3, как потенциальной, строится контур, и по нему перераспределяются корреспонденции с загрузкой потенциальной связи. Связи A2-B3 и A3-B4 (связи со знаком +) догружаются объемом по 10 ед. (минимальный для связей со знаком -), а для связей A3-B3 и A2-B4 (связи со знаком -) снимается объем по 10 ед. В результате получаем 3-е улучшенное базисное распределение (таблица 3.8).
Производим проверку полученного распределения на оптимальность. Так как в улучшенном распределении для всех свободных связей оценочные параметры sij ³ 0, то последнее решение является оптимальным.
Проверяем выполнение ограничений на размер корреспонденций. Сравнивая в последней таблице значения Xij (центр клетки связи) и Xoij (правый нижний угол клетки связи) устанавливаем, что нарушено ограничение только для связи A1-B3 (X1-3 =10>Xo1-3 =5). Для связи A1-B3 реализуем следующие действия:
в окончательное решение вводится корреспонденция X1-3 =5;
корректируются соответствующие размеры наличия и потребности в ресурсе
XА1=XА1–X1-3=10-5=5;
XB3=XB3–X1-3=20-5=15;
корректируется соответствующая стоимость (расстояние) поставки l1-3 путем замены на большое число, например l1-3 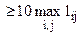 . Принимаем l1-3=80.
. Принимаем l1-3=80.
Таблица 3.8 – Распределительная таблица (3-е улучшенное базисное распределение)
| Поставщи- ки Ai | Потребители Bj | X Ai | uAi | ||||
| B1 | B2 | B3 | B4 | B5 | |||
| A1 | +1 4 | +6 8 | +77 80 | +1 80 | |||
| A2 | +2 7 | 719 800 | |||||
| A3 | +1 5 | 0 3 | |||||
| X Bj | |||||||
| uBj |
Согласно укрупненному алгоритму решения задачи следует с новыми данными вернуться на составление первоначального базисного решения (таблица 3.9).
Производим проверку полученного распределения на оптимальность. Так как в данном распределении для отдельных свободных связей оценочные параметры sij ≤ 0, то данное решение является неоптимальным.
Действуя в ранее изложенном порядке в результате многократных улучшений получаем нижеприведенное оптимальное решение (таблица 3.10).
Согласно общему алгоритму проверяем выполнение ограничений на размер корреспонденций. Поскольку объемы корреспонденций не превышают заданные ограничения на размер поставок, то решение закончено.
Таблица 3.9 – Первоначальное базисное распределение для измененных данных
| Поставщи- ки Ai | Потребители Bj | X Ai | uAi | ||||
| B1 | B2 | B3 | B4 | B5 | |||
| A1 | 0 4 | +3 8 | +75 80 | +74 80 | -719 80 | ||
| A2 | -2 4 | -2 4 | |||||
| A3 | +3 5 | -721 80 | -2 | ||||
| X Bj | |||||||
| uBj |
Таблица 3.10 – Оптимальное распределение для измененных данных
| Поставщи- ки Ai | Потребители Bj | X Ai | uAi | ||||
| B1 | B2 | B3 | B4 | B5 | |||
| A1 | +5 8 | +77 80 | +76 80 | 0 80 | |||
| A2 | +2 7 | +719 800 | |||||
| A3 | +1 5 | 0 3 | |||||
| X Bj | |||||||
| uBj |
Полное окончательное решение содержит:
ранее включенные корреспонденции в окончательное решение
X2-2 = 5;
X1-3 = 5;
и последнее решение для реальных пунктов
X1-1 = 5;
X2-1 = 5;
X2-2 = 5;
X2-3 = 15;
X3-4 = 30.
Ответ: исходя из минимума нулевых пробегов и других дополнительных условий оптимально закрепить за 1-м предприятием 1-й и 3-й маршрут с выделением по 5 единиц, за 2-м – 1-й, 2-й и 3-й с выделением соответственно 5, 10 и 15 единиц, за 3-м – 4-й маршрут с выделением 30 единиц транспортных средств.
Поиск по сайту:
