Одномерная задача динамического программирования

Задача динамического программирования – это частный случай задачи нелинейного программирования, когда решение может быть получено соответствующим методом. Одной из наиболее простых является следующая нелинейная одномерная распределительная задача.

Необходимо оптимальным образом распределить ресурс в объеме x_o по n вариантам (объектам, схемам, этапам) при целевой функции

и ограничениях

,

где x_i – объем ресурса, назначаемый по i-му варианту (0 £x_i £ x_о);

f(x)– нелинейная функция, определяющая эффект (затраты) в зависимости от значений x;

n – общее число вариантов; x_общ – общий объем распределяемого ресурса.

Этой моделью описывается задача оптимального распределения однородного ограниченного по количеству ресурса (сырья, машин, денежных средств и т.д.).

Обозначим через x_ci – количество ресурса, назначаемого суммарно по i-му варианту и всем предыдущим вариантам. При этом объем ресурса по предыдущим вариантам распределен оптимально исходя из минимума затрат или максимума эффекта.

Тогда целевая функция Z_i при рассмотрении i-го этапа решения определяется по выражению

Z_i(x_ci, x_i)= f_i(x_i) + f* _i-1 (x_ci - x_i),

где 0 £x_сi £ x_общ при i £ n-1 и x_сi= x_общ при i = n;

f*_i-1 – функция, определяющая эффект (затраты) оптимальным образом по предыдущим вариантам в зависимости от объема ресурса x_ci-1;

Значение f*_i определяется по Z_i:

для i =1 (x_c1=x₁);

, .

Определение 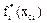и соответствующих им при данном x_сiпроизводятся поэтапно от i=2 до i=n.

По окончательному результату поэтапных расчетов формируется оптимальное решение {x_оi}:

x_оi= (для i = n);

x_оi = при (для );

(для i=1).

Вариант алгоритма решения однопродуктовой задачи динамического программирования приведен на рисунке 3.24. Решение предусмотрено для целевой функции, подлежащей оптимизации на максимум. Для решения задачи на минимум необходимо ввести исходные значения s_вji с отрицательным знаком или внести изменения в блоках 12 (заменить 1E+12 на -1E+12) и 15 (условие < на >).

Выводимые j, k_jid_x , s_nm представляют соответственно номер варианта, объем ресурса по варианту и значение целевой функции для оптимального решения.

Пример. Банковский кредит может быть использован по 4-м вариантам (n=4). Общий объем кредита x_общ = 800 тыс.ед. Дискретность распределения кредита по вариантам использования dx = 200 тыс.ед. Зависимость эффекта по вариантам использования кредита нелинейна и задана таблично (таблица 3.11).

Таблица 3.11 – Значения эффектов в зависимости от номера варианта i и объема ресурса x

Необходимо распределить кредит, чтобы суммарный эффект от его использования был максимальным.
1

Пуск

Ввод n, x_oбщ, d_x n – число вариантов распределения ресурса

x_oбщ – общий объем ресурса

d_x – дискретность распределения ресурса

m = x_oбщ/ d_x m – число разбиений ресурса

s_вji, 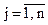; s_вji – эффект (затраты) по j-му варианту

при объеме использования ресурса x_i

5 6

s_1i = s_в1i

k_1i = i

8 Да 9 10

Нет

r = m j = n r = 1

r = m

12 18

p = 1E+12

16 19

s_ji =c _l: k_ji = l; p = c _l Вывод j, k_jrd_x

Да

Нет 15 14 20

c _l < p c _l =s_{вj l} + s_{j-1, i- l} r = r - k_jr

Вывод s_nm

Рисунок 3.24 – Алгоритм решения однопродуктовой задачи

динамического программирования 22

Останов

РЕШЕНИЕ.

Имеем целевую функцию = max;

ограничения x_{общ =} x_{1 +} x₂₊ x_{3 +} x₄ = 800; 0 £x_i £ x_общ,

а также – для одного первого варианта.

На втором этапе (i=2) рассматриваем одновременно распределение ресурса для первого и второго варианта. Результаты расчетов сводим в таблицу 3.12. Значком (*) отмечен столбец, соответствующий оптимальному значению при данном x_ci.

Таблица 3.12 – Расчет при i=2

xci

xi

xci - xi

+

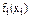
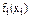12*

23*

34*

44*

44*

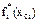
На третьем этапе (таблица 3.13) решения рассматриваются одновременно оптимальный вариант по 1-му и 2-му вариантам совместно с третьим вариантом (i=3).

Таблица 3.13 – Расчет при i=3

xci

xi

xci - xi

+

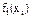
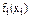12*

23*

34*

44*

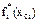
Переходим к последнему этапу (i=4). При этом x_сi = x_о (таблица 3.14).

Исходя из результатов выполнения последнего этапа расчетов следует, что кредит можно использовать с максимальным эффектом, равных 45 тыс.ед., при этом, х_о4 = 200 тыс.ед.

Тогда на 3-й и все предыдущие варианты остается 600 тыс.ед. Оптимальный объем использования кредита по 3-му варианту, как следует из этапа 3 решения, при x_{с i} = 600 равен x_о3 = 0;

на 2-й и все предыдущие остается по прежнему 800-200-0=600. Оптимальный объем использования кредита по 2-му варианту, как следует из этапа 2 решения, при x_{с i} = 600 равен x_о2 = 400.

Таблица 3.14 – Расчет при i=4

xci
xi
xci - xi
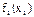
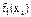+		45*

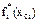
Оптимальный объем кредита к использованию по первому варианту определяется как остаток x_о1 =800-200-0-400 = 200.

Ответ: Оптимальное распределение кредита по вариантам использования следующее:

1-й – 200 тыс.ед; 2-й – 400 тыс.ед., 3-й – 0 тыс.ед; 4-й – 200 тыс.ед.

Поиск по сайту: