Задачи упорядочения и согласования

Задачи упорядочения – это задачи определения оптимальной последовательности событий, а задачи согласования рассматривают сетевое планирование и управление.

Основа решения первых – теория расписаний, вторых – теория графов.

Предметом сетевого планирования и управления (СПУ) является разработка и оптимизация сетевых графиков.

Сетевой график – это ориентированный граф, дуги которого имеют одну или несколько числовых характеристик. Дугами изображают работы, а вершинами – события.

Работа – это процесс, сопровождающийся затратами времени и ресурсов. Если имеются затраты только времени – это так называемые фиктивные работы (естественная сушка и т.п.).

Событие – это итог процесса или его части. Оно совершается, когда закончены все предшествующие ему работы.

Путь – это любая непрерывная последовательность работ от исходного события до завершающего (т.е. до конечной цели).

Длина пути определяется суммой продолжительности образующих его работ.

Рассмотрим сетевой график с одним исходным и одним завершающим событием, известными продолжительностями t _ij работ ij, где i – событие, соответствующее началу работы и j – соответственно окончанию. Общее число событий m, число работ n.

Ниже приведен пример сетевого графика (рисунок 3.30) и длительности работ (таблица 3.30).

Расчет сетевого графика включает отыскание следующих основных параметров:

ранний и поздний сроки начала работ t _р.нij и t _п.нij;

ранний и поздний сроки окончания работ T _р.оij и T _п.оij;

ранний и поздний сроки наступления событий T _рi и T _пi;

4

3

1 6

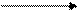
2 5

Рисунок 3.30 – Пример схемы сетевого графика

Таблица 3.30 – Дительность работ

полный и свободный резервы времени каждой работы R _пij и R _сij;

резерв времени событий R _i;

критическое время графика t _кр и перечень работ, образующих критический путь;

полный резерв R _l времени путей l, альтернативных критическому.

На основании этих характеристик определяется перечень работ, образующих критический путь – путь максимальной длины от начального до завершающего события, имеющий критическое время t _кр.

Для расчета необходимо произвести правильную нумерацию событий, т.е. для любой работы ij номер предшествующего события i должен быть меньше номера последующего события j.

Алгоритм вычислений следующий:

1) Присваивается исходному событию начальный, например, нулевой момент времени раннего срока свершения T _{рi = 1}=0;

2) Последовательно для каждого 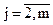рассчитываются

;

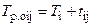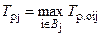
где B _j – множество событий i, соединенных работами с j- м событием.

В результате находятся Т _рi, .

3) Критическое время сетевого графика t _кр = T _рm .

4) Поздний срок свершения завершающего события принимается равным критическому t _кр или заданному директивному времени t _дир (t _дир³ t _кр ):

T _{пm =} t _кр или T _{пm =} t _дир.

5) Последовательно для каждого пункта 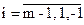рассчитываются

;

_,

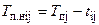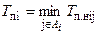где A _i – множество событий j, соединенных работами с i-м событием.

6) Рассчитываются резервы времени событий

R _i = T _пj - T _рi.

7) Рассчитываются полные резервы времени работ – максимальное время на которое можно отсрочить или увеличить продолжительность работы ij, не изменяя установленного позднего срока наступления завершающего события

R _пij = T _пj - T _р.оij= T _пj - T _рi - t _jj.

8) Рассчитываются свободные резервы времени работ – максимальное время на которое можно отсрочить или увеличить продолжительность работы ij, при условии, что все события будут выполнены в свои ранние сроки

R _сij = T _рj- T _р.оij = T _рj- T _рi – t _ij.

Величина свободного резерва меньше или равна величине полного резерва.

9) Определяется критический путь. Это путь, продолжительность которого равна критическому времени – минимальному времени, в течение которого может быть выполнен весь процесс и включает работы с нулевым полным резервом (проходит через события с нулевыми резервами).

10) Полный резерв времени интересующих альтернативных путей определяется как разность между длиной критического пути и длиной любого другого полного пути t_l

R_l = t _кр- t_l.

Пример. Рассчитать параметры приведенного выше сетевого графика. Директивное время принять равным критическому пути.

Поиск по сайту: