Гамма-функция точно определяется по формуле

, х>0.

Для гамма-функции справедливы соотношения

Г(х+1)=х Г(х); (*)

Г(1) = 1;

Г(0,5)= ;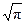

Г(n+1)= n!, n= 0,1,2,...;

Г(х) Г(-х) = -p /(х sin p x). (**)

Рассчитывают с использованием формулы Стирлинга или на основе аппроксимации.

Для x > -18 с погрешностью порядка 1Е-05 гамма-функция может быть вычислена на основе 20-кратного преобразования следующим образом:

z=21 + x;

применения формулы Стирлинга

.

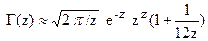последовательного уменьшения значения z на единицу до значения х и вычислений соответствующих значений гамма-функции по формуле Г(z) =Г(z+1)/ z.

Преобразование обеспечивает вычисления для отрицательных чисел x и с высокой точностью при их малых значениях.

Пример программной реализации метода:

20 CLS: INPUT "ВВЕДИТЕ x= "; Z: x = Z

30 FOR I = 1 TO 20

40 Z = Z*(x+I): NEXT I

50 B = x + 21

60 G=EXP(B*(LOG(B)-1)+1/12/B)*SQR(2*3.141519/B)/Z

70 PRINT "ЗНАЧЕНИЕ Г(x)="G

80 END

Гамма-функция на основе коррекции формулы Стирлинга определяется по формуле

,

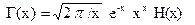где x > 1.0;

,

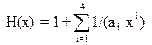где a₁= 12; a₂= 288; a₃= -139/51840; a₄= 571/2488320.

При 0<x<1 значение Г(x) с целью повышения точности находится с использованием формулы (*) Г(x) = Г(x+1)/x.

Если x<0, то гамма-функция вычисляется на основе формулы (**) как

Г(x) =-p/(z Г(z)sin pz),

где z=abs(x).

Ниже приведен пример программы на основе коррекции формулы Стирлинга:

input "x";x

if x>1 then z=x:gosub pp:goto kon

if x>0 then z=x+1:gosub pp:g3=g3/x:goto kon

if x<=-1 then z=abs(x):gosub pp:goto 10

if x<0 then z=abs(x)+1:gosub pp:z=z-1:g3=g3/z

10 g3=-3.141592/z/sin(3.141592*z)/g3

goto kon

pp:

hk=1+1/12/z+1/(288*z^2)-139/(51840*z^3)+571/(2488320*z^4)

g3= SQR(2*3.141592/z)*EXP(-z)*z^z*hk

return

kon:

print "Γ("x")= "g3

end

На основе аппроксимации определение Г(z+1) для значений z от 0 до 1 может производится с использованием степенного полинома

,

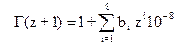где b₁= -57719165, b₂= 98820589, b₃= -89705694, b₄= 91820688, b₅= -75670408, b₆= 48219934, b₇= -19352782, b₈=3586835.

Для расчета гамма-функции по аппроксимации необходимо вычислить гамма-функцию от абсолютной величины дробной части заданного аргумента и затем на основе использования выражения (*) и, при необходимости, выражения (**) найти значение гамма-функции исходного числа.

Для вычислений интегральной функции нормального закона распределения (рисунок 2.4) применяются численное интегрирование или аппроксимации.

Для вычисления F(x) = g с точностью 0,0001 на основе численного интегрирования интервал интегрирования необходимо принимать от а-3,9s до х,

где x – значение аргумента;

a и s – параметры функций нормального закона распределения: a = x_м; s = s,

x_м –оценка математического ожидания случайной величины;

s – оценка среднеквадратического отклонения случайной величины.

Вычисление значения интегральной функции нормального распределения F(x) = g на основе аппроксимации возможно по следующему алгоритму:

1) z = (х- a)/ s,

2) ,

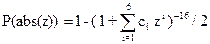где c₁= 49867347Е-09; c₂= 21141006Е-09; c₃= 32776261Е-10;

c₄= 38004Е-09; c₅= 48891Е-09; c₆= 5383Е-09;

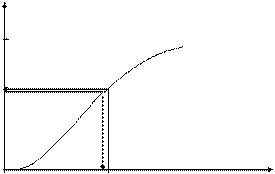3) .

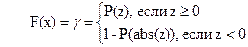1,0

g

x

Рисунок 2.4 – Функция распределения (нормальный закон)

Нахождение для нормального закона распределения по значению интегральной функции g значения аргумента x=F^-1( g ) возможно на основе аппроксимации по следующему алгоритму:

1)

2) t = (ln (1/P))^0.5;

3)

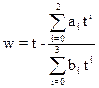
а₀= 2.515517; а₁= 0.802853; а₂= 0.010328;

в₀= 1.0; в₁= 1.432788; в₂= 0.189269; в₃= 0.001308;

4) z = - w, если g ≥0.5, иначе z = w

5) x = a + s z.

Поиск по сайту: