 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача о коммивояжере
Имеется n пунктов, в которых должен побывать коммивояжер. Задана матрица стоимостей (расстояний, времени и т.п.) на переход между пунктами cij ,  и
и 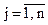 . Коммивояжер должен выйти из одного из пунктов, побывать во всех остальных пунктах по одному разу и вернуться в начальный пункт.
. Коммивояжер должен выйти из одного из пунктов, побывать во всех остальных пунктах по одному разу и вернуться в начальный пункт.
Необходимо найти порядок обхода, дающий минимальную суммарную стоимость посещения всех пунктов.
Введем переменную Kjj
 .
.
Необходимо найти множество {Kij },  и
и 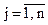 , дающее минимум
, дающее минимум

и выполнение ограничений
 ; (*)
; (*)
 ; (**)
; (**)
Ui -Uj +nK ij £ n-1, i ¹ j, (***)
где Ui, Uj – целые неотрицательные числа, представляющие собой номера этапов, на котором посещаются соответствено пункты i и j.
Условие (*) означает, что коммивояжер выходит из каждого пункта один раз, а условие (**) – что он входит в каждый пункт только один раз. Условие (***) обеспечивает замкнутость цикла (контура) только на n-м этапе решения задачи.
Задача без учета условия (***), представляет постановку, аналогичную задаче о назначениях и отличается тем, что целевая функция стремится к минимуму (Z→min). Если при ее решении получен замкнутый контур, то это оптимальное решение, а иначе полученное значение целевой функции является той оценкой, которая всегда меньше или равна целевой функции (длине пути) с учетом условия (***).
Точное решение задачи дает метод ветвей и границ, а приближенные – метод ближайшего соседа, метод сумм (изложен ранее для составления сборочно-развозочных маршрутов), метод Кларка-Райта.
Метод ветвей и границ – один из методов решения различных задач комбинаторного типа. Для решения задачи о коммивояжере применяется алгоритм Литтла.
Алгоритм метода ближайшего соседа (один из вариантов):
1) создается рабочий массив стоимостей переходов 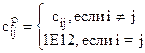 ,
,  ;
;  ;
;
2) текущее множество перемещений коммивояжера L задается нулевым (число переходов m=0). В итоге решения элементы массива L будут представлять перечень пунктов lk,  ;
;
3) находится переход коммивояжера максимальной стоимости из массива  как
как  (i¹j);
(i¹j);
4) изменяется m (m=m+1) и один из пунктов r или s, например пункт r вводится во множество L (lm=l1=r);
5) составляется путь перемещений коммивояжера:
5.1) рассматривается множество M стоимостей переходов, соединенных с пунктами l1 и lm, т.е. рассматриваются длины переходов  и
и  (lj не принадлежит множеству L);
(lj не принадлежит множеству L);
5.2) находится переход минимальной стоимости из массива М как  . Если crs=1Е12, то решение закончено (на 7), а иначе на 5.3;
. Если crs=1Е12, то решение закончено (на 7), а иначе на 5.3;
5.3) изменяется m (m=m+1);
5.4) текущее множество перемещений коммивояжера L дополняется переходом rs. Если l1=r, то lk=lk-1,  и l1= s, а если lm-1=r, то lm= s;
и l1= s, а если lm-1=r, то lm= s;
5.5) если m=2, то  =
=  = 1Е12 и на 6, а если иначе, то
= 1Е12 и на 6, а если иначе, то  =
=  = 1Е12;
= 1Е12;
5.6) если l2= r, то  =
=  = 1Е12,
= 1Е12,  , а если lm-1=r, то
, а если lm-1=r, то  =
=  = 1Е12,
= 1Е12,  ;
;
6) возврат на 5.1.
7) контур перемещений замыкается путем введения еще одного перехода коммивояжера (m=m+1 и lm= l1).
Общая стоимость замкнутого контура переходов коммивояжера  .
.
С целью упрощения алгоритм не исключает повторную замену стоимостей переходов на бесконечно большое значение (принято 1Е12).
Пример. Задана транспортная сеть, схема которой приведена на рисунке 3.28, и стоимости переходов в таблице 3.23. Необходимо решить задачу коммивояжера методом ближайшего соседа.
 2
2
1 3
Рисунок 3.28 – Схема транспортной сети
Таблица 3.23 – Стоимости переходов
| I | J | |||
Решение.
1) создается рабочий массив  ,
,  ,
, 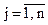 (таблица 3.24);
(таблица 3.24);
2) задается пустым текущее множество переходов коммивояжера L (число переходов m=0).
3) находится переход максимальной стоимости из массива  как
как  с2-3(i¹j);
с2-3(i¹j);
4) изменяется m на m=m+1=0+1=1 и один из пунктов, например пункт 2 вводим во множество L (lm=l1=2);
Таблица 3.24 – Рабочий массив стоимостей переходов (исходный)
| I | J | |||
| 1E12 | ||||
| 1E12 | ||||
| 1E12 | ||||
| 1E12 |
5) составляется путь перемещений коммивояжера (последняя цифра номера – номер итерации):
5.1.1) находится множество M стоимостей переходов, соединенных с пунктами l1 и lm (т.е. рассматриваются при данной итерации переходы 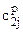 );
);
5.2.1)находится в множестве М переход с минимальной стоимостью как  с2-4=5. Так как c2-4¹1Е12, то на 5.3.1;
с2-4=5. Так как c2-4¹1Е12, то на 5.3.1;
5.3.1) изменяется m на m=m+1=1+1=2;
5.4.1) текущее множество перемещений коммивояжера L дополняется переходом 2-4. Поскольку l1=r, то lm=l2= l1=2 и l1=s=4. Имеем L={ l2=2 и l1=4};
5.5.1) поскольку m= 2, то  =
=  = 1Е12 и на 6.
= 1Е12 и на 6.
Все замены приведены в таблице 3.25 рабочего массива – 1-е изменение;
6.1) на 5.1.2;
5.1.2) находится множество M стоимостей переходов, соединенных с пунктами l1 и lm,т.е. рассматриваются звенья  и
и 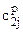 ;
;
5.2.2) находится звено минимальной стоимости из массива М как  с4-1=3. Так как c4-1¹1Е12, то на 5.3.2;
с4-1=3. Так как c4-1¹1Е12, то на 5.3.2;
5.3.2) изменяется m на m=m+1=2+1=3;
5.4.2) текущее множество перемещений коммивояжера L дополняется переходом 4-1. Поскольку l1=r=4, то lm=l3=l2=2, lm-1=l2= l1=4 и l1=s=1. Имеем L={l1=1, l2=4, l3=2};
5.5.2) поскольку m>2, то  =
=  =1Е12, т.е.
=1Е12, т.е.  =
=  = 1Е12;
= 1Е12;
5.6.2) поскольку l2 =r=4, то 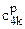 =
=  = 1Е12,
= 1Е12,  (в четвертой строке и 4-м столбце проставляются 1Е12). Все замены приведены в таблице 3.26 рабочего массива – 2-е изменение;
(в четвертой строке и 4-м столбце проставляются 1Е12). Все замены приведены в таблице 3.26 рабочего массива – 2-е изменение;
6.2) на 5.1.3.
5.1.3) находится множество M стоимостей переходов, соединенных с пунктами l1 и lm (т.е. рассматриваются звенья  и
и 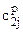 );
);
Таблица 3.25 – Рабочий массив стоимостей переходов (1-е изменение)
| I | J | |||
| 1E12 | ||||
| 1E12 | 1E12 | |||
| 1E12 | ||||
| 1E12 | 1E12 |
Таблица 3.26 – Рабочий массив стоимостей переходов (2-е изменение)
| I | j | |||
| 1E12 | 1E12 | 1E12 | ||
| 1E12 | 1E12 | 1E12 | ||
| 1E12 | 1E12 | |||
| 1E12 | 1E12 | 1E12 | 1E12 |
5.2.3) находится переход минимальной стоимости из массива М как  с1-3=5. Так как c1-3¹1Е12, то на 5.3.3;
с1-3=5. Так как c1-3¹1Е12, то на 5.3.3;
5.3.3) изменяется m на m=m+1=3+1=4;
5.4.3) текущее множество перемещений коммивояжера L дополняется звеном 1,3. Поскольку
l1=r, то lm=l4=l3=2, lm-1=l3=l2=4, lm-2=l2=l1=1 и l1=s=3. Имеем L={l1=3, l2=1, l3=4 и l4=2};
5.5.3) поскольку m>2, то  =
=  = 1Е12;
= 1Е12;
5.6.3) поскольку l2= r=1, то  =
=  = 1Е12,
= 1Е12,  .
.
Все замены приведены в таблице 3.27 рабочего массива – 3-е изменение;
6.3) на 5.1.4.
Таблица 3.27 – Рабочий массив стоимостей переходов (3-е изменение)
| I | j | |||
| 1E12 | 1E12 | 1E12 | 1E12 | |
| 1E12 | 1E12 | 1E12 | 1E12 | |
| 1E12 | 1E12 | 1E12 | 1E12 | |
| 1E12 | 1E12 | 1E12 | 1E12 |
5.1.4) находится множество M стоимостей переходов, соединенных с пунктами l1 и lm (т.е. рассматриваются переходы  и
и  );
);
5.2.4) находится переход минимальной стоимости из массива М как  1Е12 (любое звено). Так как c1-1=1Е12, то на 7;
1Е12 (любое звено). Так как c1-1=1Е12, то на 7;
7) контур перемещений замыкаем путем введения еще одного перехода (m=m+1=4+1=5 и l5= l1=3. Тогда контур перемещений коммивояжера 3-1-4-2-3, так как L={l1=3, l2=1, l3=4, l4=2 и l5=3}. Любой из пунктов может быть началом переходов данной последовательности. При этом общая стоимость замкнутого контура переходов коммивояжера С не изменится
 = с3-1+с1-4+ с4-2+с2-3 = 5+3+5+8 = 21 ед.
= с3-1+с1-4+ с4-2+с2-3 = 5+3+5+8 = 21 ед.
Задача о коммивояжере на основе алгоритма метода сумм решается в следующем порядке:
1) принимается один из пунктов за начальный (базовый);
2) считается, что все другие пункты входят в путь перемещений;
3) пункты поочередно включаются в путь перемещений по алгоритму метода сумм.
Задача о коммивояжере на основе алгоритма метода Кларка-Райта (для маршрутизации перевозок мелких партий ресурса) решается с учетом следующих условий:
1) исходный пункт – один из пунктов, принадлежащий звену с наибольшей стоимостью;
2) единичные объемы ресурса по пунктам;
3) допускаемое число промежуточных пунктов заезда не менее n-1;
4) один вид транспортного средства по вместимости и эта вместимость не менее n-1;
5) объединение отдельных маршрутов с нулевыми выигрышами до полной их взаимной увязки в один маршрут.
Пример. Решить ранее поставленную задачу на основе метода Кларка-Райта.
Решение. В качестве начального пункта принимаем пункт 2, как принадлежащий звену с максимальной длиной. Допускаемое число промежуточных пунктов не менее 3, вместимость транспортного средства – не менее трех.
Затем по алгоритму метода Кларка-Райта выполняем следующее:
1) в качестве начального пункта принимаем пункт 2, как принадлежащий звену с максимальной длиной (А=2) и строим систему маятниковых маршрутов, на каждом из которых предполагается обслуживать один пункт. Для каждого такого маршрута назначаем транспортное средство заданной вместимости (таблица 3.28).
Таблица 3.28 – Система первоначальных маршрутов
| Шифр маршрута i | Схема A-i-A | Объем ресурса | Число промеж. Пунктов ni | Вместимость трансп.средства qi |
| 2-1-2 | ||||
| 2-3-2 | ||||
| 2-4-2 |
2) рассчитываются выигрыши для всех возможных вариантов попарного объединения маршрутов, образованных согласно пункту 1.
Выигрыши рассчитываются по формуле
Dсij = сAi + сAj -сij,
где сij – величина сокращения пробега транспортного средства при объединении маршрутов A-i-A и A-j-A;
сAi, сAj – стоимость перемещения от начального пункта A соответственно до пунктов i и j;
сij – расстояние между пунктами i и j, ед.
Возможные варианты и выигрыши приведены в таблице 3.29.
Таблица 3.29 – Расчет выигрышей от попарного объединения маршрутов
| маршрут i | маршрут j | выигрыш Dсij | Примечание |
| 6+8-5=9 | -1 (3.5.1) | ||
| 6+5-3=8 | -1 (п.3.5.2) | ||
| 5+8-4=8 | -1 (п.3.4.2) |
3) последовательно производится объединение маршрутов следующим образом:
3.1.1) находим максимальный выигрыш от попарного объединения исходных маршрутов. Это два маршрута r =1 и s=3. Поскольку максимальный выигрыш >0, то переход на п. 3.2.1;
3.2.1) оцениваем возможность объединения маршрутов с учетом наличия транспортных средств необходимой вместимости и выполнения других заданных ограничений. Для возможного нового маршрута определяем общий объем перевозимого ресурса как сумму ресурсов объединяемых маршрутов Qr(s)=Qr+Qs,=Q1 +Q3= 1+1=2 и число пунктов заезда на объединенном маршруте nr(s) = nr+ns = n1+n3 =1+1=2. Если такое объединение невозможно, то переход на пункт 3.4. В нашем случае полученные параметры не превышают допускаемых и объединение возможно.
3.3.1) Формируем новый объединенный маршрут, состоящий из двух объединяемых по пунктам с найденным максимальным выигрышем. Полученный маршрут имеет вид A-1-3-A;
3.4.1)
· машруты с шифрами 1 и 3 аннулируются (Q1 =0, Q3=0);
· формируется шифр маршрута, определяемый номерами крайних пунктов (пункты 1 и 3);
· назначается объем перевозок Q1(3)= 2 и число промежуточных пунктов заезда n1(3)=2;
· назначается транспортное средство, удовлетворяющее условию  =3;
=3;
· поскольку nr(s) =2 то далее;
· поскольку не выполняется nr>1 и ns>1, то на 3.5.1;
3.5.1) реальное значение выигрыша с1-3 заменяется отрицательным (с1-3= -1);
3.6.1) переход на 3.1.2;
3.1.2) находим максимальный выигрыш от попарного объединения исходных маршрутов. Это два маршрута r=1 и s=4. Поскольку выигрыш не отрицательный – то решение не закончено;
3.2.2) оцениваем возможность объединения маршрутов с учетом наличия транспортных средств необходимой вместимости и выполнения других заданных ограничений. Для возможного нового маршрута определяем общий объем перевозимого ресурса как сумму ресурсов объединяемых маршрутов Qr(s)=Qr+Qs,=Q1 +Q4 =2+1=3 и число пунктов заезда на объединенном маршруте nr(s) = nr+ns = n1+n4 =2+1=3. Полученные параметры не превышают допускаемых и объединение возможно.
3.3.2) Формируем новый объединенный маршрут, состоящий из двух объединяемых по пунктам с найденным максимальным выигрышем. Полученный маршрут имеет вид A-4-1-3-A;
3.4.2)
· машруты с шифрами 1(3) и аннулируются (Q1(3) =0, Q4=0);
· формируется шифр маршрута, определяемый номерами крайних пунктов (пункты 4 и 3);
· назначается объем перевозок Q4(3)= 3 и число промежуточных пунктов заезда n4(3)=3;
· назначается транспортное средство, удовлетворяющее условию  =3;
=3;
· поскольку nr(s) >2, то на -1 заменяется выигрыши между пунктами маршрута 4 и 3 (Dc3,4=-1);
· поскольку выполняется nr>1, то Dc1i= -1,  ;
;
3.5.2) реальное значение выигрыша с1,4 заменяется отрицательным (с1,4= -1);
4) переход на 3.1.3;
3.1.3) находим максимальный выигрыш от попарного объединения исходных маршрутов. Это два маршрута r =1 и s=3. При этом максимальный выигрыш отрицательный и поэтому решение закончено.
В результате получен следующий путь коммивояжера: 2-4-1-3-2, который совпал с путем 3-1-4-2-3 (с обходом пунктов в обратном порядке), полученным методом ближайшего соседа (длина пути 21 ед.).
Метод Кларка-Райта как и метод "ближайшего соседа" не гарантирует получение оптимального решения. Такое решение обеспечивает метод ветвей и границ.
Алгоритм простейшей реализации метода ветвей и границ следующий:
1) принимается один из пунктов за начальный пункт ветвления, например, один из пунктов, принадлежащих переходу с наибольшей стоимостью (длиной). Стоимость (длина) ветвления у начального пункта принимается равной нулю;
2) из пункта с минимальной стоимостью ветвления (минимальной текущей оценкой границы ветвления) производятся ветвления (включение переходов), не дающие замкнутого цикла (в ветви отсутствуют пункты с одинаковыми номерами кроме последнего n-го шага ветвления по каждой ветви) и рассчитываются стоимости ветвления у вновь включенных в ветви пунктов; каждая ветвь на n-м шаге замыкается на начальный пункт. Стоимость ветвления у вновь включенных пунктов рассчитывается по формуле Zji=Zj,i -1 + ci, где Zji и Zj,i-1– соответственно оценка стоимости j-й ветви на шаге i и i-1;ci – стоимость перехода, включаемого в ветвь на i-м шаге;
3) находится минимальное значение из всех рассчитанных стоимостей дерева ветвления. Если какая-то ветвь имеет число переходов (звеньев) n и минимальное значение стоимости ветвления, то оптимальное решение получено, а иначе необходимо продолжать ветвление (переход на п. 2).
Одна из ветвей с минимальным значением стоимости ветвления у конечного пункта и включающая все n пунктов, дает решение.
Пример. Решить ранее поставленную задачу методом ветвей и границ.
Решение. В качестве начального пункта принимаем пункт 2, как принадлежащий звену с максимальной длиной.
Порядок ветвления и оценка стоимостей ветвей показаны на нижеприведенном рисунке (в треугольнике даны номера пунктов, в квадрате текущие стоимости ветвления и возле линий звеньев их длины).
Получены оптимальные решения (2-1-3-4-2 или 2-4-3-1-2) с Z=20, которые дают оптимальный путь на 1 ед. менее ранее полученных. Это значит, что решение предыдущими методами не обеспечило оптимальное решение.

0 2
6 5 8
6 1 4 5 3 8
9 4 3 5 3 4 5 4 4 12
11 3 8 1 3 9 1 13
4 4 5 5 3 3
13 3 15 4 3 13 14 1 4 6 1 15
8 5 8 6 5 6
21 2 20 2 2 21 20 2 2 21 2 21
Рисунок 3.29 – Пример решения задачи о коммивояжере методом ветвей и границ
Поиск по сайту: