Исследование временных рядов

Временной ряд представляет собой значения показателя в зависимости от времени. Может представлять изменение показателя по годам, за год по месяцам, за неделю по дням, за сутки по часам и т.п. Временной ряд может быть моментным (показатель зафиксирован на какие-то моменты времени) или интервальным (показатель зафиксирован за промежутки времени).

Временной ряд может выравниваться различного рода зависимостями (степенными, показательными, параболическими, логарифмическими, гиперболическими и др.).

Временные ряды с периодическими изменениями наиболее часто описываются рядом Фурье. Таким периодическим изменениям подвержены многие физические и экономические явления, связанные с сезонной, недельной, суточной и другой изменчивостью. Например, имеется такая изменчивость по дням недели для транспортной подвижности населения и нет зависимости от дня недели для температуры воздуха. Выражения, связывающие фактор (время) и зависимую переменную, имеют следующий вид:

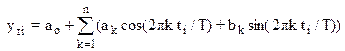или

,

где y _тi – значение теоретической функции в i-й расчетной точке;

a_о – свободный член уравнения;

n – верхнее значение номера гармоники ряда Фурье;

k – номер гармоники;

a_k, b_k – коэффициенты ряда Фурье при k-й гармонике соответственно при cos и sin;

t _i – значение фактора (времени) в i-й расчетной точке;

T – интервал времени, за который рассматривается временной ряд;

m – общее число чисел во временном ряду.

Вторая формула может применяться только для случая, когда показатели зафиксированы через равные интервалы времени, а первая – в любом случае.

Параметры (коэффициенты) уравнений определяются соответственно по следующим зависимостям:

или

;

или

,

где y_эi – экспериментальные значения зависимой переменной в i-х расчетных точках.

Проверка адекватности полученного уравнения (многочлена ряда Фурье) экспериментальным данным производится по критерию Фишера и средней линейной ошибке аппроксимации. При этом при расчете числа степеней свободы под числом факторов понимается число использованных гармоник ряда Фурье.

При проведении расчетов номера гармоник, включаемые в уравнение, рекомендуется принимать адаптивно по максимуму значения статистики критерия Фишера F или минимуму средней линейной ошибки аппроксимации E. Гармоники, которые вызывают уменьшение значения F или увеличение значения E, не включаются в модель связи. При этом верхнее значение номера гармоник не должно быть больше чем m/2.

Компьютерная программа выравнивания динамических рядов с помощью многочлена ряда Фурье приведена в приложении 6.

Поиск по сайту: