Численное интегрирование

Численное интегрирование – это вычисление определенного интеграла

на основе многократных вычислений значений f(x). Применяется, если функция F(x) не может быть определена аналитически.

Такой интеграл численно равен площади фигуры, ограниченной ординатами в точках a и b, осью абсцисс и линией графика подинтегральной функции f(x) (рисунок 2.3).

Для численного интегрирования отрезок [a, b] разбивается на m частей, к каждой из которых применяется аппроксимация выбранной функцией (прямой, параболой, полиномом и т.п.).

Существует ряд методов численного интегрирования: прямоугольников, модернизированный прямоугольников, трапеций, Ньютона-Котеса (аппроксимация полиномом Лагранжа), Симпсона (аппроксимация параболой), Уэдлля (разбивка каждого из m отрезков на 6 частей), Чебышева (с неравномерным разбиением аргумента), Симпсона (кубатурная аппроксимация), Гаусса (кубатурная аппроксимация), Ромберга, Бодэ и др.

По методу прямоугольников интеграл вычисляется по формуле

,

где x(i) = a + (i-1) h или x(i) = a + i h; h = (b - a)/m.

Модернизированный метод прямоугольников отличается правилом выбора расчетных точек x(i):

x(i) = a + h/2 + (i-1) h.

f(x)

S

a i=1 2 3 4 5 6 b x

Рисунок 2.3 – Графическая интерпретация численного интегрирования

По методу трапеций

,

где x(i) = a + i h.

Рассмотренные методы являются по сравнению с другими более простыми, но менее эффективными.

В качестве примера более эффективного (точного) метода рассмотрим метод Ньютона-Котеса. Этот метод базируется на применении к каждому i-му из m отрезков разбиения следующей формулы:

,

где x(j) = x(i) + j h / 6;

x(i)= a + (i -1) h;

d(0)= d(6)= 41;d(1)= d(5)= 216;d(2)= d(4)= 27;d(3)=272.

Значение интеграла S находится суммированием значений S_i :

.

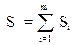Вариант программной реализации алгоритма последнего метода приводится ниже.

10 REM МЕТОД НЬЮТОНА-КОТЕСА

15 CLS

20 INPUT"a";a

30 INPUT"b";b

40 INPUT"m";m

45 DIM d(6)

47 d(0)=41:d(1)=216:d(2)=27:d(3)=272:d(4)=27:d(5)=216:d(6)=82

50 h=(b-a)/m:E=h/6

70 FOR I=1 TO m

72 XT=a+(I-1)*h

75 FOR J=0 TO 6

80 X=XT+J*E:GOSUB 200

90 SI=SI+d(J)*F

100 NEXT J

110 NEXT I

130 SI=SI*H/840

140 PRINT"SI="SI:GOTO 300

200 F=………………..:RETURN

300 END

Ошибка определения значения интеграла зависит от величины h и производной k-го порядка от интегрируемой функции в точке, где она максимальна (для первых трех методов k=2 и для Ньютона-Котеса k=8).

Поиск по сайту: