 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Численное решение дифференциальных уравнений
Приняв h = 0,1 методом Эйлера решить задачу Коши для каждого из уравнений. Найти точное решение, построить график.
| В-1 | 
| 
| 
|
| В-2 | 
| 
| 
|
| В-3 | 
| 
| 
|
| В-4 | 
| 
| 
|
| В-5 | 
| 
| 
|
| В-6 | 
| 
| 
|
| В-7 | 
| 
| 
|
| В-8 | 
| 
|  ;1] ;1]
|
| В-9 | 
| 
| 
|
| В-10 | 
| 
| 
|
Найти изображение функций-оригинала.
1. 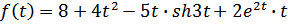 ;
;
2. 
3. 
4.  ;
;
5. 
6.  ;
;
7. 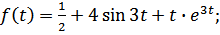
8. 
9.  ;
;
10.  .
.
20. Найти оригиналы, для данных изображений:
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  .
.
Решить ДУ операторным методом
| 1. | 
| 
| 
|
| 2. | 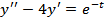
| 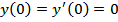
| |
| 3. | 
| 
| 
|
| 4. | 
| 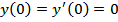
| |
| 5. | 
| 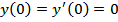
| |
| 6. | 
| 
| 
|
| 7. | 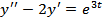
| 
| 
|
| 8. | 
| 
| 
|
| 9. | 
| 
| 
|
| 10. | 
| 
| 
|
Найти область сходимости степенного ряда
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
Разложить в ряд Фурье функцию
| 1. | 
| 

|
| 2. | 
| 

|
| 3. | 
| 

|
| 4. | 
| 
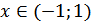
|
| 5. | 
| 

|
| 6. | 
| 

|
| 7. | 
| 

|
| 8. | 
| 

|
| 9. | 
| 

|
| 10. | 
| 

|
24. Для функций f (x), заданной таблицей найти  а также их значения в точке x = x 0. Составив многочлен Лагранжа.
а также их значения в точке x = x 0. Составив многочлен Лагранжа.
| х | |||
| у |
1.
| х | |||
| у |
2.
| х | -2 | -1 | |
| у |
3.
| х | -1 | -2 | |
| у |
4.
| х | -2 | -1 | |
| у |
5.
| х | |||
| у | -10 |
6.
| х | -3 | -2 | -1 |
| у |
7.
| х | -1 | ||
| у |
8.
| х | -3 | -2 | -1 |
| у |
9.
| х | -1 | ||
| у | -14 | -6 |
10.
Поиск по сайту: