АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение системы с использованием обратной матрицы

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. I. Формирование системы военной психологии в России.
  3. II. Решение логических задач табличным способом
  4. II. Цель и задачи государственной политики в области развития инновационной системы
  5. II. Экономические институты и системы
  6. III. Разрешение споров в международных организациях.
  7. III. Решение логических задач с помощью рассуждений
  8. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  9. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  10. SCADA-системы
  11. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  12. SWOT- анализ и составление матрицы.

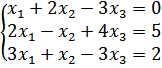
Составим три матрицы:

– из коэффициентов при неизвестных.

– столбцовая из неизвестных.

– из свободных членов.

Систему можно записать в виде: , матрица Х находится . Т.о., чтобы найти матрицу 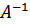обратную для матрицы А. Находим определитель матрицы А:

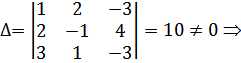А невырожденная.

Составим алгебраические дополнения элементов матрицы А:


;

;

;

;

;

;

;

;

.

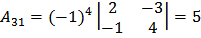Составим матрицу из полученных алгебраических дополнений.

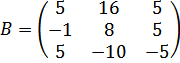
Составим , заменив строки столбцами:

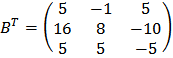
Обратную матрицу 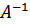составим по формуле , т.о.

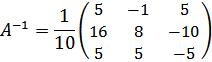
Найдем матрицу Х:

,


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

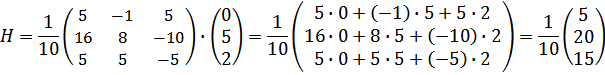
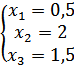
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)