 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ОБРАЗЦЫ ВЫПОЛНЕННИЯ ЗАДАНИЙ
Задание 1: Вычислить определитель
| -1 | |||
| -1 |
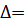
Решение: Умножим третью строку на -1 и прибавим к четвертой:
| -1 | |||
| -1 |
|
| -1 |
| = |
разлогая полученный определитель по элементам четвертой строки, мы должны умножить ее элементы на соответствующие алгебраические дополнения. Но так как три элемента из 4-х равны 0, то из всей суммы останется лишь второе слагаемое:
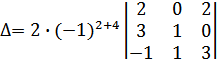 , минор получен вычеркиванием 4-ой строки и 2-го столбца в пересечении которых расположен элемент 2≠0. Алгебраическое дополнение этого элемента равно минору
, минор получен вычеркиванием 4-ой строки и 2-го столбца в пересечении которых расположен элемент 2≠0. Алгебраическое дополнение этого элемента равно минору  .
.
Умножим на  и на сам элемент 2, т.е.
и на сам элемент 2, т.е.
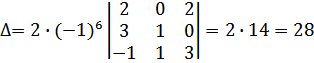
Определитель третьего порядка:
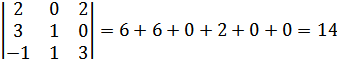 , вычислен по правилу треугольника.
, вычислен по правилу треугольника.
Задание 2: Даны две матрицы А и В. Найдите А × В; В× А; А × А -1, А -1 × А.

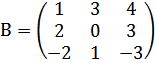
Решение: Умножив по очереди строки матрицы А на столбцы В, получим:
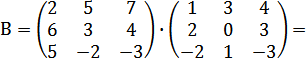
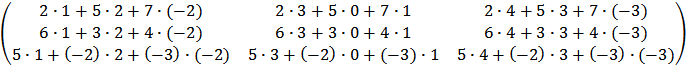
 .
.
Аналогично находим произведение:
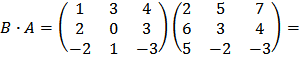
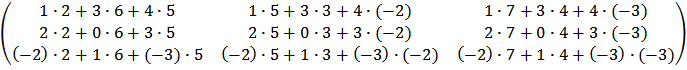
 .
.
Чтобы найти А × А -1 и А -1 × А нужно сначала получить матрицу А -1 – обратную для матрицы А.
Находим определитель матрицы А,
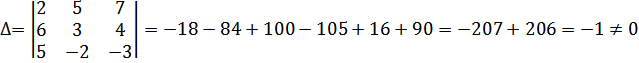 , значит данная матрица невырожденная.
, значит данная матрица невырожденная.
Вычислим алгебраические дополнения элементов матрицы А:
 ;
;
 ;
;
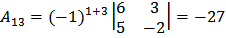 ;
;
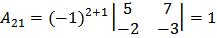 ;
;
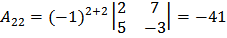 ;
;
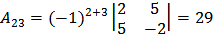 ;
;
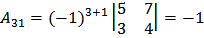 ;
;
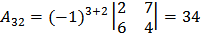 ;
;
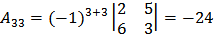 ;
;
Составим вспомогательную матрицу
 ,
, 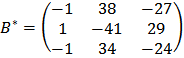 .
.
Составим 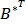 , заменив в матрице
, заменив в матрице  строки столбцами:
строки столбцами:
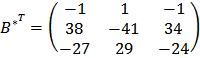
Cоставим А -1 по формуле 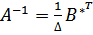
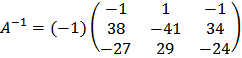

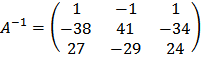 .
.
Вычислим произведения А × А -1 и А -1 × А.
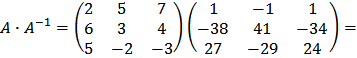

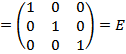

 .
.
Задание 3: (Решение системы линейных уравнений) Докажите, что данная система совместна, для этого составим две матрицы: основную А и расширенную матрицу В.
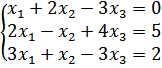
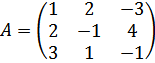 составлена из коэффициентов при неизвестных
составлена из коэффициентов при неизвестных
 расширенная матрица.
расширенная матрица.
Находим ранг матрицы А и матрицы В, используя элементарные преобразования матриц.
Подвергнем матрицу А следующим элементарным преобразованиям: первую строку прибавим ко 2-ой, в результате получим матрицу:

в полученной матрице вторую строку умножим на (-1) и прибавим к 3-ей, получим
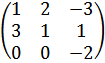
теперь первый столбец умножим на (-2) и прибавить ко 2-ому, затем 1-ый столбец умножим на (3) и прибавим к 3-ему
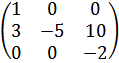
первую строку умножаем на (-3) и прибавляем ко 2-ой
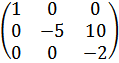
третью строку умножаем на 5 и прибавляем ко 2-ой

второй столбец умножаем на 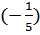 , третий на
, третий на 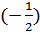 получим матрицу
получим матрицу
 .
.
Следовательно ранг матрицы А равен 3, т.е. r (А) = 3.
| -2 |
| -1 |
| + |
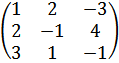

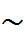
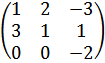
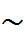

|

|
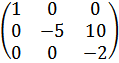

 Þ
Þ
r (А) = 3 (по количеству единиц по главной диагонали).
| -2 |
| -1 |
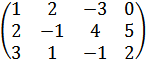
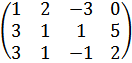

| + |
| + |
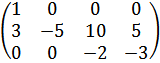
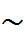
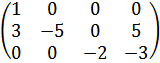
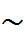

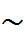
| -3 |
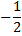
|

|

|
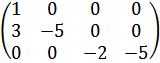
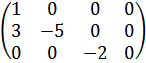
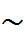

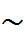
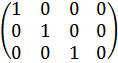
 r (В) = 3.
r (В) = 3.
Таким образом, т.к. r (А) = r (В), то система совместна, т.е имеет хотя бы одно решение.
В силу тог, что число неизвестных n = 3 и выполнения условия r (А) = r (В) = n, то решение будет единственное.
Поиск по сайту: