Примерный перечень вопросов к экзамену. 1. Определение матрицы, виды матриц

1. Определение матрицы, виды матриц. Определитель матрицы.

2. Доказать свойства определителя матрицы:

§ замена строк столбцами;

§ пропорциональность строк (столбцов);

§ вынесение общего множителя за знак определителя.

3. Определение минора и алгебраического дополнения.

4. Разложение определителя по элементам строки (столбца).

5. Определение ранга матрицы.

6. Линейные операции с матрицами, линейные отображения.

7. Произведение матриц, обратная матрица.

8. Доказать, что А × А^-1 = А^-1 × А = Е.

9. Совместимость системы линейных уравнений. Теорема Кронекера-Капелли.

10. Матричная форма записи системы линейных уравнений.

11. Решение систем с помощью матриц: по формулам Крамера, методом Гаусса.

12. Определение вектора, коллинеарность, компланарность векторов.

13. Линейные операции с векторами.

14. Определение скалярного произведения и его свойства:

§ доказать, то ;

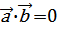§ доказать, что ;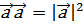

доказать, что 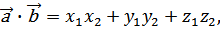где ; .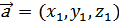

15. Базис, координаты вектора в базисе, векторное пространство Евклидово пространство.

16. Вывести общее уравнение прямой на плоскости и плоскости в пространстве.

17. Уравнение прямой через две точки; через точку в дано направлении; с угловым коэффициентом.

18. Уравнение плоскости через три данные точки.

19. Уравнение прямой в R³.

20. Взаимное расположение:

§ прямых на плоскости;

§ плоскостей в пространстве;

§ прямой и плоскости в пространстве.

21. Каноническое уравнение кривых 2-го порядка.

22. Понятие множества, числовые множества, объединения, пересечения множеств.

23. Группы, кольца и поля. Топология множеств.

24. Множество действительных чисел и его подмножества.

25. Определение комплексного числа, геометрический смысл, различные формы записи комплексного числа. Действия с комплексными числами.

26. Понятие функции, основные характеристики функции, понятие функционального анализа.

27. Основные элементарные функции и их графики.

28. Определение предела последовательности функции, геометрическая иллюстрация.

29. Основные теоремы о пределах.

30. Определение беконечномалых и их свойства.

31. Приращение аргумента и функции.

32. Непрерывность точки разрыва и их классификация.

33. Определение производной, правила и формулы дифференцирования.

34. Частные производные.

35. Исследование f (x) на возрастание, убывание, выпуклость, вогнутость.

36. Экстремумыфункции, одной и двух переменных.

37. Вектор-фукция и ее дифференцирование, элементы дифференциальной геометрии.

38. Первообразная, основная теорема о первообразных.

39. Определение неопределенного интеграла и его свойства.

40. Определение определенного интеграла и его свойства.

41. Понятие несобственного интеграла.

42. Формула Ньютона-Лейбница. Методы интегрирования.

43. Дифференциальные уравнения первого порядка, общее, частное решение.

44. Дифференциальное уравнение 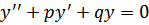и его решение.

45. Определение фундаментальной системы решений.

46. Определение преобразования Лапласа.

47. Свойства преобразования Лапласа:

§ линейности

§ подобия

§ дифференцирование оригинала

§ теорема смещения

§ теорема запаздывания

48. Уравнение в частных производных, уравнения математики, физики.

49. Числовые ряды. Сумма ряда, сходимость ряда.

50. Необходимый признак сходимости.

51. Признак Лейбница.

52. Достаточные признаки сходимости рядов (без доказательства).

53. Функциональные ряды: степенные, ряд Фурье.

54. Элементы гармонического анализа.

55. преобразования Фурье.

Поиск по сайту: