 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение системы методом Гаусса

Используя элементарные преобразования систем, сведем данную систему к специальному виду:
1 шаг – преобразуем систему так, чтобы все коэффициенты при 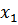 были равны 1, для этого второе уравнение делим на 2, третье на 3:
были равны 1, для этого второе уравнение делим на 2, третье на 3:
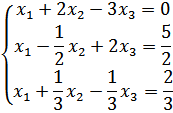
2 шаг – вычтем первое уравнение из второго и третьего:

3 шаг – делим второе уравнение на  и третье на
и третье на  :
:
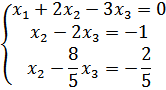
4 шаг – второе уравнение вычтем из третьего:
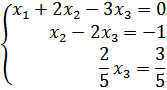
5 шаг – из третьего уравнения находим х 3, 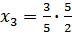
 и подставляем во второе:
и подставляем во второе:
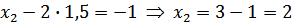
6 шаг – значения х 3 и х 2 подставляем в первое уравнение и находим х 1, 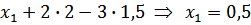 .
.
Ответ: 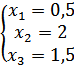 .
.
Задание 4: (Элементы векторной алгебры и аналитической геометрии)
S (1;1;2) A (2;3;-1) B (2;-2;4) C (-1;1;3)
1 Используя формулы
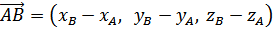 и
и
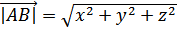 , получим
, получим
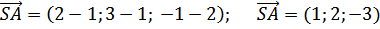





2 Используем уравнения через две точки:

Т.к. координаты точек А; В; С известны, получим АВ, 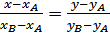
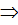

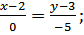
Обозначим 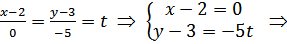
 – параметрические уравнения стороны АВ.
– параметрические уравнения стороны АВ.
АС: 

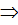

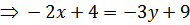
 – уравнение стороны АС
– уравнение стороны АС
ВС: 

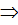
 ,
, 
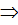
 – уравнение стороны ВС.
– уравнение стороны ВС.
3 Для определение угла А, применим формулу
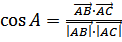 , получим
, получим
 ;
;
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  ;
;
 ;
;
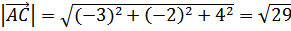 .
.


4. Для составления уравнения плоскости r АВС, применим уравнения плоскости, проходящей через три данные точки А (2;3;-1) В (2;-2;4) С (-1;1;3).
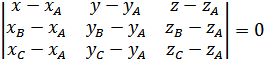 , подставив координаты точек, получим
, подставив координаты точек, получим
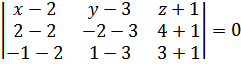 , разлагаем по элементам первого строчки
, разлагаем по элементам первого строчки




 уравнение плоскости r АВС.
уравнение плоскости r АВС.
5. Условие перпендикулярности прямой и плоскости имеет вид:
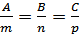 , где А; В; С – координаты нормали плоскости треугольника АВС, т.е
, где А; В; С – координаты нормали плоскости треугольника АВС, т.е 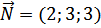 , m; n; p – координаты направляющего вектора,
, m; n; p – координаты направляющего вектора,  прямая перпендикулярная плоскости r АВС, значит
прямая перпендикулярная плоскости r АВС, значит  , тогда
, тогда
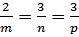 , значит
, значит
m = 2; n = 3; p = 3. Высота проходит через вершину S (1;1;2), уравнения прямой, проходящей через точку:
 ,
,
Зная m; n; p получим
 – уравнение высоты.
– уравнение высоты.
1. Исходя из геометрического смысла векторного произведения, имеем
 .
.
Найдем вектора, на которых построен треугольник АВС,
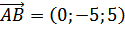

Составим векторное произведение:
 , разложим по элементам первой строки (см. 4)
, разложим по элементам первой строки (см. 4)
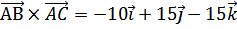
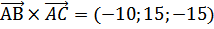
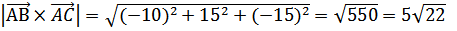 (ед).
(ед).
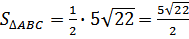 (ед2).
(ед2).
2. Введем в рассмотрение векторы:
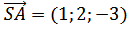
 (см. 1)
(см. 1)

Объем пирамиды, построенной на векторах  , равен
, равен
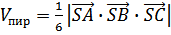 ,
,


 (ед3)
(ед3)
3. Т.к.  , то
, то 
 (ед3)
(ед3)  ед2), тогда
ед2), тогда
 (ед).
(ед).
| X |
| Z |
| Y |
| -2 |
| -1 |
| -2 |
| -1 |
| B |
| S |
| С |
| А |
Задание 5: (Л инейное программирование) Фирма выпускает два вида мороженого: сливочное и шоколадное. Для приготовления мороженого используются два продукта: молоко и наполнители. Расходы которых на 1 кг мороженого и суточные запасы даны в таблице:
| Исходный продукт | Расход на 1 кг мороженого | Запас кг | |
| Сливочное | Шоколадное | ||
| Молоко | 0,8 | 0,5 | |
| Наполнители | 0,4 | 0,8 |
Изучения рынка сбыта показало, что суточный спрос на сливочное мороженное превышает спрос на шоколадное не более, чем на 100 кг, спрос на шоколадное не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного – 16 ед, шоколадного – 14 ед. Определить количество сливочного и шоколадного мороженного, которое должна производить фирма чтобы доход от реализации продукции был максимальным.
Решение:
1. Формализация задачи;
2. Составление математической модели;
3. Решение математической модели;
4. Совершенствование математической модели, т.е. анализ математической модели и ее модернизация.
1. Формализация задачи.
Обозначим: х1 – суточный объем выпуска сливочного мороженого, х2 – шоколадного.
Целевая функция 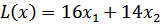 .
.
Ограничения:

2. Математическая модель.
Найти максимум функции 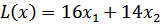 в области рений системы ограничений:
в области рений системы ограничений:
 (*)
(*)
3.
| x 1 |
| L |
|
| I |
| II |
| III |
| M |
| E |
| D |
| F |
| O |
| B |
| A |
| x 2 |
| IV |
Область допустимых решений многоугольник OABDEF. Строим вектор 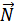 , используя функцию
, используя функцию 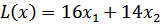 Þ
Þ 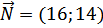 .
.
Строим линию уровня 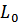 ,
,  . Перемещаем
. Перемещаем 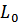 в направлении вектора
в направлении вектора 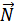 , до положения опорной прямой, в данной задаче опорная прямая проходит через точку D.
, до положения опорной прямой, в данной задаче опорная прямая проходит через точку D.
Находим координаты точки D или по чертежу, или решая систему уравнений:

D (312,5; 300) – оптимальное решение, т.е.  при этом
при этом  .
.
Т.о. максимальный доход от реализации продукции составляет 9200 ед. в сутки при выпуске 312,5 кг сливочного и 300 кг шоколадного мороженного.
Задание 6: Выполните действия и результат изобразите геометрически.
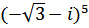
Решение: Сначала найдем тригонометрическую форму числа 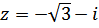 , определим модуль числа z,
, определим модуль числа z, 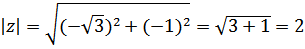 ;
;
| j |
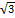
|
| -1 |
| x |
| y |
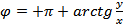
 Þ
Þ 

Применив формулу:

получим
 или
или

| -16 |
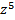
|
| z |
| -1 |

|

|
| y |
| x |
Выполните действия:

Умножим числитель и знаменатель дроби, на число, сопряженное знаменателю:

Рассмотрим извлечение корня:
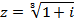
Число  представим в тригонометрической форме. Модуль числа
представим в тригонометрической форме. Модуль числа  равен
равен

Аргумент  ;
;  Þ
Þ  .
.
Тригонометрическая форма
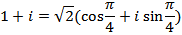
Для вычисления  используем формулу:
используем формулу:
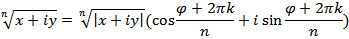
Т.о.
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Получим три различных значения корня:
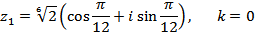


| y |

|
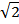
|

|

|
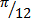
|
| -1 |
| x |
| z1 |
| z2 |
Задание 7: Установить точки разрыва функции
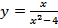 .
.
Решение: Данная функция является дробно-рациональной и поэтому она непрерывна во всех точках, в которых знаменатель отличен от нуля. В точках х 1= 2; х 2 =-2 функция не определена. Рассмотрим односторонние пределы функции в этих точках:
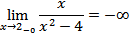
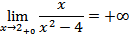
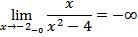
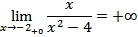
Следовательно, х = 2, х = -2 точки разрыва второго рода.
Установим наличие асимптот. График функции 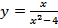 имеет вертикальные асимптоты х = 2, х = -2, т.к.
имеет вертикальные асимптоты х = 2, х = -2, т.к.
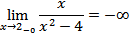
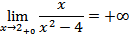
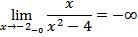
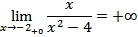
Уравнение наклонной асимптоты имеет вид  , где
, где

Найдем k
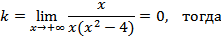
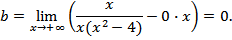
Т.о. уравнение наклонной асимптоты y =0. Асимптоту y =0 – называют горизонтальной.
Задание 8: Построить плоские фигуры, ограниченные линиями.
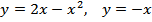 .
.
Решение:  – парабола, ось симметрии параллельна оси ОУ, ветви направлены вверх. Найдем точки пересечения с осью ОХ, т.е решим уравнение:
– парабола, ось симметрии параллельна оси ОУ, ветви направлены вверх. Найдем точки пересечения с осью ОХ, т.е решим уравнение:

 Þ
Þ 
 – прямая, биссектриса второго и четвертого координатных углов. Найдем точки пересечения параболы и прямой, т.е. решение уравнения:
– прямая, биссектриса второго и четвертого координатных углов. Найдем точки пересечения параболы и прямой, т.е. решение уравнения:
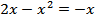

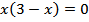
 Þ
Þ 
 Þ
Þ 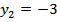
Т.о. точки пересечения параболы и прямой A (0;0), B (3;-3)
| -1 |
| -2 |
| -3 |
| A |
| B |
Задание 9: Построить график функции

Решение: Область определения f (x) состоит из трех промежутков:
(-¥; -2], в этом промежутке f (x) = 0
(-2; 0], в этом промежутке f (x) = 
(0; +¥], в этом промежутке f (x) = 1.
| -2 |
| -1 |
| х |
| y |
Задание 10: (Дифференцирование функций) Найдите  , если
, если  .
.
Решение: Применяя правило, дифференцирования дроби
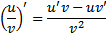
И также формулы  и
и  , находим
, находим
 или
или  ;
;
Найти  если
если  .
.
Применяя правило дифференцирования произведения  и формулы
и формулы  получим
получим

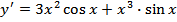 .
.
Найти  если
если  .
.
Применяя правило дифференцирования сложной функции:
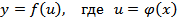
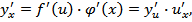
А также формулы 
 , получим
, получим
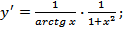
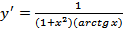 .
.
Задание 11: Исследовать функцию и построить график
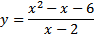
Решение: Находим область определения 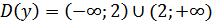 , точка х =2 не входит в область определения. Найдем односторонние пределы функции:
, точка х =2 не входит в область определения. Найдем односторонние пределы функции:
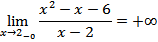

Т.о. х =2 точка разрыва второго рода, а уравнение х =2, есть уравнение вертикальной асимптоты. Составим уравнение наклонной асимптоты  , где
, где

 ;
;
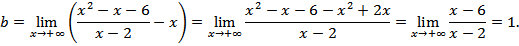
Т.о. уравнение наклонной асимптоты 
| -1 |
| x |
| y |
| y=x+1 |
Исследовать на возрастание, убывание и экстремумы.

 .
.
Найдем критические точки
 Þ
Þ 
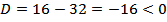 . Значит действительных корней нет. Знак
. Значит действительных корней нет. Знак 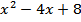 совпадает со знаком коэффициента при х 2 в данном случае коэффициент при х 2 равен 1>0, значит
совпадает со знаком коэффициента при х 2 в данном случае коэффициент при х 2 равен 1>0, значит  при любых
при любых  . y возрастает на всей
. y возрастает на всей  .
. 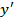 не существует, если знаменателем равен 0, т.е.
не существует, если знаменателем равен 0, т.е.  , эта точка не входит в
, эта точка не входит в  Þ функция не имеет экстремумов.
Þ функция не имеет экстремумов.
Найдем точки перегиба

| y |
 при х <2, в (-¥;2) график выпуклый, точек перегиба нет, т.к. х =2 не входит в
при х <2, в (-¥;2) график выпуклый, точек перегиба нет, т.к. х =2 не входит в  . Строим график
. Строим график
| x =2 |
| y = x +1 |
| -1 |
| х |
Задание 12: Исследовать функцию двух переменных на экстремумы
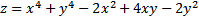
Решение: Частные производные первого порядка:


Приравнивая эти производные к нулю, получим систему уравнений:
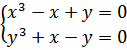 ,
,
решая систему найдем стационарные точки. Складывая уравнения, получим:

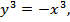
 , подставим в первое уравнение системы:
, подставим в первое уравнение системы:


 , тогда
, тогда
 , т.о.
, т.о.
имеем три стационарные точки P 1(0;0), P 2( ), P 3(
), P 3( ).
).
Проверим эти точки на экстремумы с помощью достаточных условий. Для этого сначала найдем частные производные второе порядка:

Подставляя координаты стационарных точек получим в точке P 1(0;0): 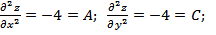
 .
.
Составим выражение
 .
.
Ответа нет, нужно дополнительное исследование.
В точке P 2( :
: 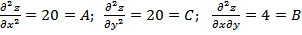
 экстремум есть, т.к. А > 0, C > 0 в точке P 2 минимум.
экстремум есть, т.к. А > 0, C > 0 в точке P 2 минимум.
 .
.
В точке P 3( ):
): 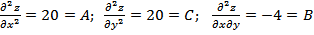 .
.
 ; А > 0, C > 0 в точке P 3 минимум.
; А > 0, C > 0 в точке P 3 минимум.  .
.
Задание 13: (Численное дифференцирование) Для функции f (x), заданной таблицей, вычислить значение этой функции и ее первой производной в указанной точке х = х 0, составив интерполяционный многочлен Лагранжа.
| х | ||||
| у |
х 0 = 2,5
Решение:
1. Составим вспомогательный многочлен:


2. Найдем 

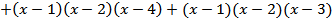
Найдем значения  в узлах интерполяции
в узлах интерполяции

 ;
;  ;
;  .
.
3. Составим многочлен Лагранжа по формуле:
 ;
;
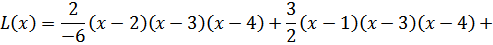
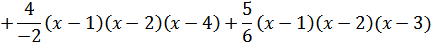

 ; в любой точке
; в любой точке
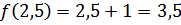
Производная по направлению, градиент  , найти
, найти 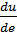 в направлении вектора
в направлении вектора  , М 0 (1;1;2), М (3;4;0), и grad u в точке М 0.
, М 0 (1;1;2), М (3;4;0), и grad u в точке М 0.
Найдем частные производные и их значения в точке М 0:

 .
.
Составим вектор  ;
; 
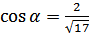 ;
;  ;
;  ,
,


grad u = 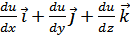
grad u = – 
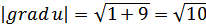
Задание 14: Вычисление интегралов
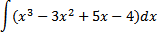
Решение: Используя свойства интеграла и формулу  получим
получим

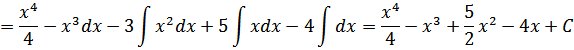

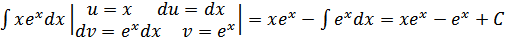 , использовали формулу
, использовали формулу
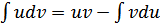



 .
.
Задание 15: Найти площадь плоской фигуры. Фигура ограничена линиями:
 .
.
Решение: Сделаем чертеж:
 – прямая,
– прямая,
 – парабола, ветви направлены вниз, ось симметрии х = 1.
– парабола, ветви направлены вниз, ось симметрии х = 1.
| m |
| B |
| O |
| A |
| y |
| х |
| y = –x |
Парабола пересекает ось ОХ в точках, которые получим, решив уравнение

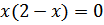

Найдем координаты точки В решив систему уравнений:
 , получим
, получим


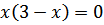

B (3;-3).
Искомая площадь состоит из двух частей,  – криволинейная трапеция
– криволинейная трапеция  .
.


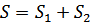
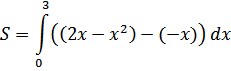
 (ед 2)
(ед 2)
Задание 16: (Численное интегрирование) Вычислить данный определенный интеграл по:
Ø формуле Ньютона- Лейбница;
Ø формулам прямоугольников;
Ø формуле трапеций.
Решение: По формуле трапеций отрезок интегрирования разбиваем на 10 частей:
 ; [1;2] a = 1; b = 2.
; [1;2] a = 1; b = 2.
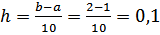 .
.
Расчет вести с тремя знаками после запятой. Составим таблицу [1;2] разбиваем на 10 равных частей:
| хk | 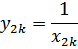
| 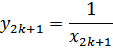
| yk |
| x0 = 1 x1 = 1,1 x2 = 1,2 x3 = 1,3 x4 = 1,4 x5 = 1,5 x6 = 1,6 x7 = 1,7 x8 = 1,8 x9 = 1,9 x10 = 2,0 | у0 = 1,000 у2 = 0,833 у4 = 0,714 у6 = 0,625 у8 = 0,556 у10 = 0,500 | у1 = 0,909 у3 = 0,769 у5 = 0,667 у7 = 0,588 у9 = 0,526 | у0 = 1,000 у1 = 0,909 у2 = 0,833 у3 = 0,769 у4 = 0,714 у5 = 0,667 у6 = 0,625 у7 = 0,58 у8 = 0,556 у9 = 0,526 у10 = 0,500 |
| å | 4,228 | 2,959 | 7,687 |
По формуле Ньютона- Лейбница:
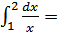 ln x
ln x 
По формулам прямоугольников:

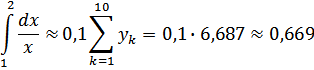
По формулам трапеций:

Формула трапеций дает более точный результат, ошибка
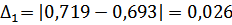

 .
.
Т.о. формула трапеций дает результат с точностью до 0,001.
Задание 17: Решить дифференциальные уравнения:
1. 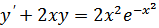 – линейное дифференциальное уравнение первого порядка.
– линейное дифференциальное уравнение первого порядка.
Решение: решение будем искать в виде  , тогда
, тогда 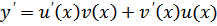 , подставив y и y ’ в уравнение, получим:
, подставив y и y ’ в уравнение, получим:

 , положим
, положим 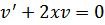 , тогда
, тогда 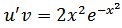 .
.
Решение данного уравнения свелось к решению системы двух уравнений с разделяющимися переменными:
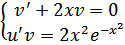
Решаем первое уравнение системы: 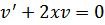 , заменим
, заменим 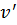 на
на 
 , разделяем переменные
, разделяем переменные
 ,
, 
Проинтегрируем обе части уравнения:
 , отсюда
, отсюда 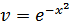 ,
,
полученное решение подставим во второе уравнение системы:
 , преобразуем
, преобразуем 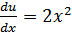 , отсюда
, отсюда  , интегрируя получим
, интегрируя получим  , находим общее решение
, находим общее решение 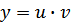 ,
,
 .
.
2.  ,
,  – однородные дифференциальные уравнения с постоянными коэффициентами.
– однородные дифференциальные уравнения с постоянными коэффициентами.
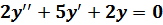
Составляем характеристическое уравнение:
 ,
,
Корни его:
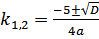 ;
; 
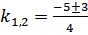 ;
;  ;
; 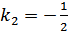
действительные разные, поэтому
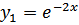 ,
,  .
.
Общее решение данного уравнения:
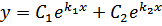
 .
.

– составляем характеристическое уравнение 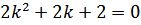 , находим его корни
, находим его корни

>  ; >
; > 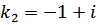 , корни комплексно-сопряженные, поэтому
, корни комплексно-сопряженные, поэтому

Общее решение данного уравнения:
 или
или

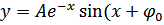 ), где
), где
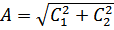 ;
;  ;
; 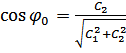
Задание 18: (Нахождение изображения по оригиналу) Найти изображение функции:
1. 
Решение: Используя таблицу оригиналов и изображений, получим
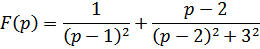
Использовали формулы:

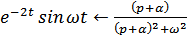 .
.
2. 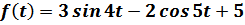

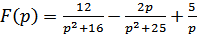 .
.
Задание 19: Нахождение оригинала по изображению:
1. 
Решение: преобразуем изображение
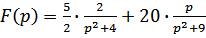 , тогда
, тогда
используя таблицу оригиналов и изображений, получим:
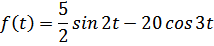
2. 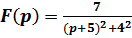
преобразуем F (p), выделив полный квадрат в знаменателе

 , тогда
, тогда
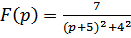 или >
или >  , тогда
, тогда
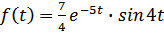 .
.
3. 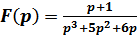
Разложим знаменатель на множители
 ,
,
где р = –2 и р = –3 корни многочлена 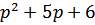 , дроби принимают вид
, дроби принимают вид

применим теорему разложения
 ;
; 
 .
.
Корни знаменателя р 1 =0, р 2 = –2, р 3 = -3 – простые действительны.
Составим таблицу:
| Рk | F1 (pk) | F2’ (pk) | 
|
| Р1 = 0 Р2 = –2 Р3 = –3 | – –2 | –2 | 


|
Найдем оригинал по формуле:
 , т.е
, т.е
 ,
,
 +
+ 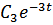 , т.о.
, т.о.
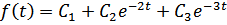 .
.
Задание 20: Решить дифференциальное уравнение операторным методом
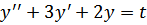 ,
, 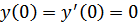
Решение: Пусть искомая функция y (t) имеет изображение 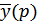 , тогда используя свойства преобразования Лапласа, получим
, тогда используя свойства преобразования Лапласа, получим



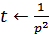 .
.
Составим вспомогательное уравнение, заменив  и t их изображениями:
и t их изображениями:
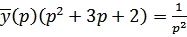 , откуда
, откуда
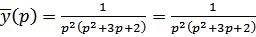 ,
,
т.к. 
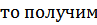
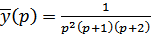 – изображение искомого решения
– изображение искомого решения 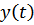 .
.
Чтобы найти 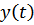 разложим дробь
разложим дробь  на простейшие:
на простейшие:
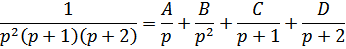
В правой части приведем к общему знаменателю:

Приравниваем числители:
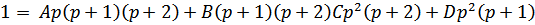
Чтобы найти А, В, С, D придавая р различные значения, будем получать:
p = 0 1 =2 B Þ B 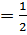
p = –1 1 = C Þ C 
p = –2 1 =-4 D Þ D 
p = 1  или
или
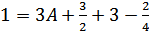 отсюда А
отсюда А  .
.
Т.о.

Тогда используя таблицу оригиналов и изображений, получим:
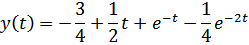
Задание 21: (Численное решение дифференциальных уравнений (метод Эйлера)) Найти приближенное, при х =1, значения решения уравнения
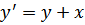
Удовлетворяющего начальному условию при х0 =0, y0 = 1.
Решение: Разделим отрезок [0;1] на 10 равных частей, h = 0,1; значения y 1, y 2, …, y n будем искать по формуле 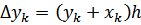 или
или
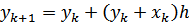 , т.о.
, т.о.
 т.о.
т.о.
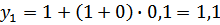
 =1,22 и т.д.
=1,22 и т.д.
В процессе решения составляем таблицу:
Поиск по сайту: