Принятие решений в условиях определенности при векторном критерии

Принятие решений в условиях определенности характеризуется детерминированными связями между принятыми решениями и полученными результатами.

Однако при этом может быть несколько критериев, по которым необходимо принимать решение. Возникает задача принятия решений при "векторном критерии". Множество всех оптимальных точек по отдельным критериям называется областью компромиссов или областью решений по Парето.

Требование одновременной максимизации (минимизации) всех частных критериев обычно несовместимо, так как при увеличении (уменьшении) одного из них могут снижаться (увеличиваться) другие. Для нахождения решения при многокритериальной оптимизации требуется перейти от задачи векторной оптимизации по частным критериям z₁, z₂,...,z_p к специально сконструированной скалярной функции Z_о, аргументами которой являются эти частные критерии. Процесс образования скалярной функции, являющейся обобщенным критерием для задач многокритериальной оптимизации, называется свертыванием или объединением векторного критерия.

Теория исследования операций предлагает ряд способов формирования обобщенного критерия Z_о по набору частных z_i.

Для параметрических критериев ниже приводится ряд способов их объединения.

Способ 1

Критерий Z_о является взвешенной суммой частных критериев z_i

,

где k_i – весовой коэффициент i-го критерия.

Неравнозначность частных критериев z_i оценивается весовыми коэффициентами k_i, что позволяет формировать с помощью данного критерия различные цели. Однако при применении такого критерия возможно, что при оптимальном решении экстремальное значение Z_о достигается при большом отклонении какого-то частного критерия z_i от своего оптимального значения. Для исключения данной ситуации могут вводиться ограничения. Весовые коэффициенты могут быть безразмерными или размерными (при различной размерности z_i), положительными и отрицательными (при свертывании критериев типа z_i® max и z_i ® min).

Способ 2

Критерий Z_о основан на минимизации абсолютных отклонений частных критериев от их экстремальных значений

,

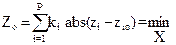где – при минимизации и

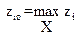– при максимизации.

Способ 3

Критерий Z_о состоит в минимизации относительных отклонений частных критериев от их экстремальных значений без учета весовых коэффициентов (применяется при различных видах экстремума, отсутствии информации о важности критериев или при различной их размерности)

.

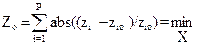Способ 4

Критерий Z_о формируется как взвешенная сумма частных критериев с учетом установленных ограничений. Тогда

,

где

Поиск по сайту: