Решение систем нелинейных уравнений

Задача состоит в нахождении корней следующей системы уравнений

f _i(X) = 0 }, ,

где X = { x₁, x₂,...,x_m}.

Для решения могут применяться следующие методы:

метод простых итераций;

метод Зейделя, отличающийся от метода простых итераций тем, что уточненные значения x_i сразу подставляются в последующие уравнения;

на основе методов поиска экстремума многомерных функций и др.

Метод простых итераций состоит в реализации процесса по следующей формуле:

x _{i (k+1)} = F_i(X_k),

где F_i(X) = f _i(X) + x _i =x _i;

i – номер переменной;

k – номер итерации.

Итерации выполняются до тех пор, пока сохраняется хотя бы по одному из x _i условие

abs (x _i(k+1) - x _i(k)) > E,

где Е – заданная точность.

Метод обеспечивает сходимость, если ¶F _j(X) / ¶x _i <1, , .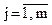

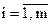Графическая интепретация метода приведена на рисунке 2.1, а схема алгоритма на рисунке 2.2.

f_i(X)+x_i,

x_i f_i(X)+x_i

x_i

x_рi x_i

Рисунок 2.1 – Графическая интерпретация метода простых итераций (x_рi – решение)

Решение с применением методов поиска экстремума (оптимизации) многопараметрических функций основано на том, что формируются функции вида

или (*)

(**)

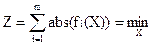где f _i(X)=0, .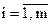

Сходимость в большой степени определяется тем методом, который будет применен для поиска минимума функции Z. Для решения системы уравнений минимальное значение функции Z должно быть равно нулю. Это условие является необходимым и достаточным. Если Z не равно нулю, то это указывает или на отсутствие решения или на неэффективный метод поиска минимума. При применении свертывания уравнений в функцию по (*) быстрее сходимость и ниже точность решения, а для функции (**) наоборот.

1

Пуск

2

Ввод m, E, m – число переменных и уравнений

x(i), 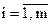E – точность поиска

x(i)– начальные (текущие) приближения Х

F(i)=f_i(X)+ x(i)

для i от 1 до m

L=1 L – признак окончания расчетов

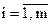
6 Нет

abs(F(i)-x(i))>E

Да

L = 0

x(i) = F(i)

Нет 9 10

L = 1 Да Вывод x(i),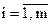

11 Рисунок 2.2 – Схема алгоритма

Останов метода простых итераций

Поиск по сайту: