 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оптимизация при наличии ограничений
В отличие от безусловной оптимизации в данном случае установлены ограничения в виде равенств и (или) неравенств в зависимости от X.
В этом случае задача состоит в поиске экстремума функции
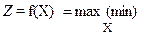, X = {xi}, 
при выполнении ограничений вида
Oj = j j(X) <= >bj,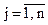 
.
Аналитическое решение задачи при ограничениях типа равенства и дифференцируемости оптимизируемой функции возможно по методу Лагранжа. Для этого вводятся множители Лагранжа lj и с их применением формируется функция L по выражению:
,
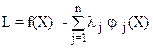где j j(X)=0.
Оптимальные значения вектора X определяются системой m+n уравнений:
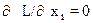} m – уравнений
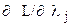} n – уравнений
ПРИМЕР.
Z = 0.5 (x2 - x1) 2 + (1 - x1)2 = min
x1 + x2 = 4 или
x1 + x2 - 4 = 0
L = 0.5 (x2 - x1)2 + (1 - x1)2 - l (x1 + x2 - 4) = 0
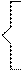
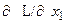= 0.50 . 2 . (x2 - x1) (-1) + 2 . (1-x1) (-1) - l = 0
= 0.50 . 2 . (x2 - x1) - l = 0
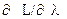= -(x1 + x2 - 4) = 0
Решение системы уравнений дает следующее решение:
x1 = 1.67; x2 = 2.33 и l = 0.67.
Без учета ограничений аналитический метод дает решение в точке x1 = 1.0; x2 = 1.0.
Графическое представление полученных решений приведено на рисунке 3.16.
В случае, если ограничения имеют вид неравенств, необходимые условия нахождения экстремума (минимума) функции f(X) при ограничениях j j (X) £ bj следующие:
ограничения в виде неравенств преобразуются в ограничения в виде равенств путем добавления дополнительных (ослабляющих) переменных 
к виду:
;
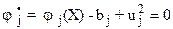формируется функция L с применением множителей Лагранжа
;
и система уравнений, решение которой определяет точку оптимума
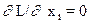} m – уравнений
} n – уравнений
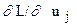} n – уравнений.
Условия решения такой задачи известны как условия Куна-Такера.
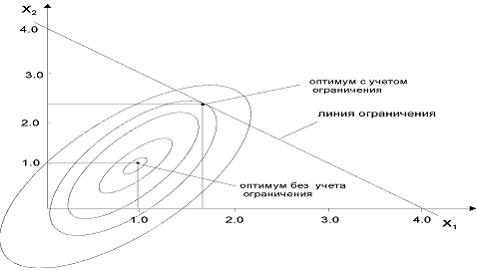
Рисунок 3.16 – Графическое представление решения по методу Лагранжа
При использовании для условной оптимизации численных методов нулевого порядка может применяться прямой учет ограничений. Для этого достаточно при оптимизации присваивать целевой функции значение далекое от экстремального, если ограничения нарушаются, например, при поиске минимума – бесконечно большие значения. Однако такой метод не всегда обеспечивает правильное решение, т.к. ограничения создают "овражность".
Для получения эффективных и надежных методов требуются более сложные процедуры. Одним из методов решения является модификация метода Нелдера-Мида, разработанная Боксом (назван комплексным методом). Метод основан на выборе 2m точек, удовлетворяющих ограничениям, и называемых комплексом.
Метод прямого учета ограничений успешно может быть применен при реализации методов случайного поиска (рисунок 3.17). Для прямого учета ограничений достаточно в подпрограмме расчета целевой функции присваивать, если хотя бы одно из ограничений нарушено, бесконечно большое (при минимизации) или бесконечно малое (при максимизации) значение. При этом данное испытание при случайном поиске не должно учитываться счетчиком неудачных проб. Если ни одно из ограничений не нарушено, то вычисляется реальное значение целевой функции.
Например, на Бейсике подпрограмма без учета ограничений и с учетом ограничений будет при оптимизации на минимум следующей:
| m1: ' п/п вычисления Z без учета ограничений Z= … Return | m1: ' п/п вычисления Z с учетом ограничений if (ограничение 1 нарушено) then m2 if (ограничение 2 нарушено) then m2 ……….. if (ограничение n нарушено) then m2 Z= …:goto m3 m2: Z= 1E20 m3: return |
Пуск
Ввод m, e m – число оптимизируемых переменных;
e – относительная точность поиска
Ввод xнi,xвi, xнi и xвi – соответственно нижняя и верхняя
начальные границы поиска оптимума
Ввод h, aш ,bш, l h –относительный шаг поиска; l – предельное
число неудачных попыток по каждой переменной;
5 aш и bш – соответственно коэффициент уменьшения
шага поиска и определения шкалы поиска
L = l m
si = (xвi - xнi)/ bш
8 на минимум
xтi = (xвi + xнi)/2 15 16
xпi= xтi Zп > Z Да xпi = xтi,
Zп= Z
Нет
9 17 11
Z = f(Xт) k = k + 1
18 Да
· Zп = Z k <= L 12
Нет
11 19
k = 0 16,21 h = h aш
12 18 20 Да 21
i = 1, m h >= e aш Вывод xпi,
Zп, h
Нет
13 22
xтi = xпi + si h (2 r -1) Вывод Zп,xпi, 11
14 Останов
Z = f(Xт)
Рисунок 3.17 – Алгоритм многомерной оптимизации
случайным поиском с пересчетом
Задача с ограничениями может быть сведена к задаче без ограничений с помощью штрафных функций. Идея внутренних штрафных функций состоит в преобразовании целевой функции Z = f(X)= min и ограничений j j (X) > 0 (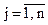) в функцию вида
Zш = f(X) + Pш 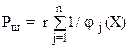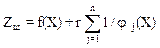=min; 
;
=min,
где r – положительная малая величина; Pш – дополнительная штрафная функция.
Если значения Х близкие или равные ограничению, то происходит резкое изменение (увеличение) функции Zш (образуется "гребень" с крутыми краями). Графическая интерпретация приведена ниже на рисунке 3.18.
2 1
Zш
x
Рисунок 3.18 – Графическая интепретация метода штрафных функций:
1 – линия ограничения; 2 – функция Zш при большем значении r; 3 – функция Zш при меньшем значении r
Значения r принимаются малыми, чтобы влияние штрафной функции Pш было меньшим в точке оптимума. При меньших значениях r хуже сходимость, при больших значениях – ниже точность решения. Поэтому r необходимо изменять в ходе оптимизации.
Существует метод внешних штрафных функций, когда штрафуется удаление от допускаемой области.
Поиск по сайту: