Комплексная оптимизация режима

Оптимизация режима может проводиться отдельно для активных и реактивных мощностей как и было рассмотрено. Однако точное решение можно получить, одновременно оптимизируя P и Q. Дополнительная экономия получается при этом за счет более точного учета режима. В качестве целевой функции в этой задаче принимаются расходы топлива на тепловых станциях

.

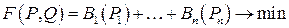При учете баланса активной мощности можно, выделив мощность балансирующей ТЭС

,

определить составляющие градиента по всем неизвестным мощностям:

;

.

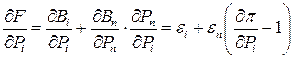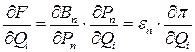Таким образом могут быть найдены все составляющие градиента в исходном приближении 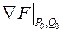и организован спуск к решению в соответствии с процедурой градиентного метода.

Точность определения определяется производным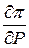и и , зависящими от режима. Производные потерь в текущей точке на каждом шаге оптимизации определяются по результатам расчета стационарного режима. В результате расчета прежде всего определяются напряжения U_i во всех узлах. По найденным напряжениям U_i можно определить потери в каждой ветви по её проводимости g_{ij ,} напряжениям по концам ветви и их сумму:

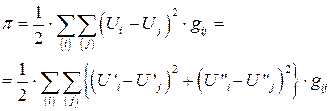
Из условия баланса мощностей для каждого узла могут быть найдены:

, , , .

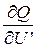С другой стороны производные потерь по составляющим напряжений, например, можно определить как 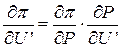, а также . Аналогично, 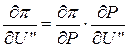и .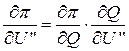

В результате можно составить следующую СЛАУ:

Решение системы A×X = B позволяет найти 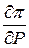и , которые используются для точного определения составляющих градиента.

Разработаны программы, реализующие этот метод, при этом градиентный метод может сочетаться с методом Ньютона.

Комплексная оптимизация по сравнению с раздельной оптимизацией может давать дополнительный эффект в пределах 0,1 ¸ 0,5 %.

Поиск по сайту: