Градиентный метод

Возможное направление выбирают противоположным градиенту:

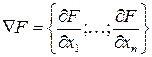
Основное уравнение:

.

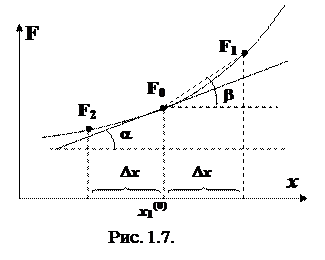Составляющие градиента 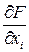находятся через конечные приращения (рис.1.7):

.

Так как tgb ¹ tga, то этот метод имеет погрешность в определении градиента, которая зависит от величины приращения аргумента.

Для снижения погрешности используют метод центрированных приращений.

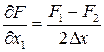
Градиентный метод часто сочетается с выбором оптимального шага. Для выбора используется пробный шаг t_0, в конце которого определяются координаты Х1 и составляющие градиента. По значениям градиента в точках Х и Х1 определяется шаг близкий к оптимальному. Алгоритм метода приведена рис.1.8.:

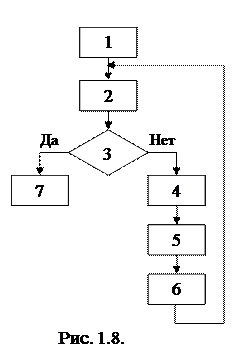
1. Исходное приближение Х = Х⁽⁰⁾;

2. Определение градиента ÑF |_X;

3. Сравнение |ÑF| < eps;

4. t₀ и определение ;

5. Определение t_ОПТ;

6. Определение ;

7. Выход.

Метод широко используется в программах оптимизации режимов.

Поиск по сайту: