Методы безусловной оптимизации

Пусть задана целевая функция F(Х)®min без ограничений, где Х={x₁,…,x_n}.

Если F(x) задана аналитически, то условие экстремума

где i= 1,…,n.

Как известно, условие минимума:

Далее будем рассматривать численные методы решения, которые удобны для реализации на ЭВМ. На сегодняшний день большинство таких методов относятся к методам возможных направлений (рис.1.5).

Расчет начинается с исходного приближения x₀. В точке x₀ рассматривается несколько направлений . Направления, ведущие к снижению F (здесь 1 и 3) называют возможными направлениями (ВН).

По любому из этих возможных направлений осуществляется переход в следующую точку: 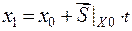, где t – шаг.

Получаем общее уравнение: ,

где k – номер итерации (шага).

Величина шага t определяет сходимость процесса:

· если t®0, то сходимость медленная, но надежная;

· если t – большой, то сходимость быстрая, но процесс может расходиться.

Наилучшая сходимость обеспечивается выбором t_ОПТ по критерию F(Х)®min на выбранном направлении . Оптимальный шаг можно выбрать, если F(x) представить по возможности как

и по условию минимума

найти оптимальный шаг .

Чаще f(t) аппроксимируют кривой второго порядка:

Для определения параметров a,b и c считают f в трех точках:

- при t = 0, когда x = x₀ (F(x₀) = F₀);

- при t = 1, (F(x₁) = F₁);

- при t = 2, (F(x₂) = F₂).

После этого составляют систему уравнений,

из решения которой находят a,b и c.

Из условия минимума функции

определяют оптимальный шаг

,

Методы, в которых определяется t_ОПТ, называются методами скорейшего поиска. Эти методы широко используются при решении задач.

В зависимости от выбора возможных направлений различают несколько методов.

Поиск по сайту: