Определение дискретных рядов аварийного выхода и снижения нагрузки

Вероятности, составляющие основу дискретных рядов, определяются методами теории вероятностей. Случаи аварийного выхода нескольких блоков из группы однотипных определяются биномиальным распределением. Рассмотрим систему из трех однотипных блоков n = 3, имеющих разные показатели надежности p_i, q_i. Сформируем сумму вероятностей всех возможных состояний системы:

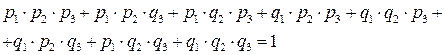
При одинаковых показателях сумма упрощается и представляется как разложение бинома третьего порядка:

.

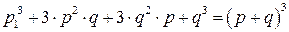Для n агрегатов вероятности всех событий определяются разложением бинома n- го порядка:

.

Вероятность выхода k агрегатов из n однотипных определяются по формуле Бернулли:

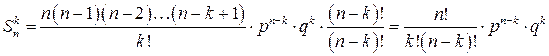
Пример:

В системе 4 блока по 50 МВт, e = 50 МВт, q = 0,01. Определить дискретный ряд аварийного выхода.

;

;

;

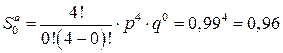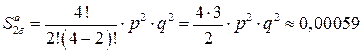При наличии в составе системы нескольких групп однотипных агрегатов вероятности выхода различной мощности, например в ke МВт, определяются из произведения биномов

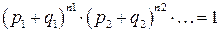
путем выбора таких слагаемых, в которых произведения определяют вероятности аварийного выхода ke МВт.

Пример:

В составе системы 3 группы однотипных блоков 2´100 + 2´50 + 4´25

с показателями надежности , , .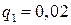

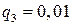Дискретный ряд вероятностей аварийного выхода определяется произведением 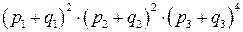= 1.

Величина дискретной ступени e = 25;

Определим несколько первых членов ряда

;

;

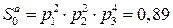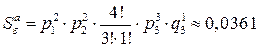аварийный выход 50 МВт возможен в двух случаях (1´50 или 2´25)

.

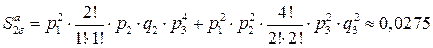Аналогично определяются все остальные члены ряда, сумма которых достаточно быстро приближается к 1.

Дискретный ряд вероятностей снижения нагрузки определяется на основе обработки суточных графиков для характерных суток и формирования годового графика по продолжительности (рис.1.50)

Полученный график заменяется ступенчатым при сохранении площади под графиками, которая пропорциональна энергии. Продолжительность ступеней и определяет соответствующие вероятности при T = 8760

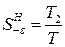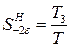, ; и т.д.

Поиск по сайту: