Метод приведенного градиента

Здесь исходный вектор неизвестных делится на два блока

X ={ c, Y }, где c – свободные, в количестве k, а Y – зависимые, в количестве m.

При этом зависимость Y(c) безусловно существует, но в неявной форме, то есть не определяется аналитическим выражением.

Выражение для градиента целевой функции можно записать по правилу вычисления производной с учетом неявных функций.

,

где в скобках указаны производные, взятые с учетом только явной зависимости.

Производную 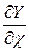можно определить аналогично из условия G(X)=0.

Поскольку G(X) = G(c,Y) = 0, то .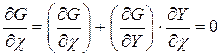

Откуда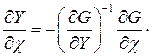

и ,

где – приведенный градиент.

Приведенный градиент может использоваться в процедуре градиентного метода.

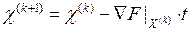
Изобразим на графике процесс поиска решения методом приведенного градиента в пространстве 2-х переменных (рис.1.11).

Здесь – это проекция антиградиента на линию ограничений, в общем случае – на плоскость.

Решение лежит в точке A, где линия ограничения касается ближайшей линии F = const.

Сложности метода связаны с определением проекции, для чего требуется обращение матрицы , имеющей размерность m´m.

Поиск по сайту: