Многомерная безусловная оптимизация

Многомерная оптимизация заключается в поиске экстремума функции нескольких (n) переменных Z= f(X) = f(x₁, x₂,..., x_n).

Для решения такой задачи применяются аналогично одномерной оптимизации аналитический метод, численные методы и методы случайного поиска.

Аналитический метод основывается на 1-х и 2-х частных производных по оптимизируемым параметрам:

¶ Z/¶ x_i = 0 }, .

Решение системы уравнений ¶ Z/¶ x_i = 0 }, дает оптимальное решение X_п, если оно существует.

Вид экстремума определяется значением определителя D матрицы Гессе

, , .

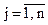Если решение существует в точке X_п и в этой точке D > 0, то оптимизируемая функция имеет минимум, а иначе максимум.

Среди численных методов различают методы нулевого порядка и градиентные (1-го и 2-го порядка). Первые основаны только на вычислениях значений оптимизируемой функции. Вторые используют частные производные соответствующего порядка. Эффективность процедуры поиска оптимума – возможность отыскания решения и сходимость к решению по скорости зависят от применяемого метода и вида функции.

Наиболее известны следующие методы нулевого порядка:

координатного спуска – поочередная оптимизация параметров вдоль осей одним из известных одномерных методов (одна из реализаций – метод Гаусса-Зейделя на основе шагового метода);

спирального координатного спуска;

вращающихся координат (метод Розенброка);

конфигураций;

Хука-Дживса с поиском по образцу;

параллельных касательных (метод Пауэлла);

Нелдера-Мида – поиска по деформируемому многограннику за счет его отражения, растяжения и сжатия и др.

1

Пуск

Ввод a, b, e a и b – начальные значения нижней и верхней

границ интервала поиска экстремума;

e – относительная точность поиска

h, L, a_ш ,b_ш h –относительный шаг поиска; L – граничное число

неудачных попыток; a_ш и b_ш – соответственно

коэффициенты уменьшения шага поиска и

определения шкалы поиска

s = (b - a)/ b_ш

x_т = (a+ b)/ 2 x_т – текущая расчетная точка

x_п= x_т x_п – текущее (начальное) приближение к решению

Z = f(x_т)

7 на минимум

11 15

Z_п = Z Z_п > Z Да x_п = x_т: Z_п= Z

15,18

k = 0 12 8

k = k + 1

x_т = x_п+ s h (2 r -1) 13

Да 13

k <= L

10 9

Z = f(x_т) 14 Нет

h = h a_ш

18 Да

8 x_п, Z_п, h h >= e a_ш

Нет

Вывод x_п, Z_п

Останов

Рисунок 3.11 – Алгоритм одномерного случайного поиска с пересчетом

Наиболее известными являются такие градиентные методы как наискорейшего спуска и Давидона-Флетчера-Пауэлла (ДФП) с использованием кубической интерполяции.

Для случайного поиска применяются метод с пересчетом, метод с парными пробами, метод по наилучшей пробе и др.

Эффективная оптимизационная процедура должна успешно решать тестовые задачи, которыми могут быть:

функция Розенброка

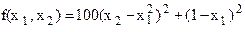
Х_п = (1;1);

функция Пауэлла

Х_п = (0;0;0;0);

двумерная экспоненциальная функция:

,

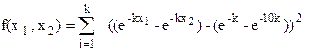при k = 1 Х_п = (1;10).

Одним из методов нулевого порядка – метод координатного спирального спуска. Основывается на поочередном приближении к решению с текущим значением шага по всем оптимизируемым переменным. Если с текущим шагом в данном направлении оптимизация вызывает "ухудшение" целевой функции, то шаг уменьшается и направление поиска меняется на противоположное. Коэффициент a_ш рекомендуется принимать равным 0.25 – 0.40. Решение продолжается до тех пор, пока шаг по модулю не станет равным или менее заданной точности решения. Алгоритм метода координатного спирального спуска приведен ниже.

Метод координатного спуска недостаточно эффективен для поверхностей с "оврагами", так как в этом случае получение решения с требуемой точностью не гарантировано. Это вызвано тем, что в случае "оврага", повернутого относительно осей, попытка продвижения в любом направлении может вызывать "ухудшение" целевой функции. В то же время продвижение вдоль "оврага" может давать "улучшение" целевой функции. Для таких случаев необходимо применять другие методы, например, метод Розенброка или метод Пауэлла.

Метод вращающихся координат (метод Розенброка) имеет следующий алгоритм (рисунок 3.13):

1) принимается начальное (текущее) приближение к решению – точка X_п1 и начальный (текущий) шаг поиска;

2) находится одним из известных методов при текущем значении шага следующее приближение – точка X_п2;

3) по линии X_п1 - X_п2 принимается новое направление поиска (производят поворот осей);

4) модифицируется шаг поиска и вдоль новых осей Z₁ и Z₂ находится следующее текущее приближение;

5) если результат с заданной точностью получен, то решение закончено или иначе по последнему и предпоследнему приближениям находится новое направление поиска и делается переход на пункт 4.

Для выполнения поворота осей используют ортогонализацию по Граму-Шмидту.

Пуск

2

Ввод m, h, a_ш, e m – число оптимизируемых переменных;

h – начальный шаг поиска; a_ш– коэффициент уменьшения

шага поиска; e – точность поиска

3

x_{п i} – начальные (текущие) приближения к решению

Ввод x_{п i},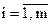

4

Z = f(X_п)

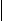5 12

10

Вывод x_пi,

Z, h

6 11 Нет

abs(h) > e

x_пi = x_пi + h

Да

12

7

Z_п = Z h = –a_ш h

8

Z = f (X) 5 13

Вывод x_пi,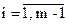

x_{п m} =x_{п m} -h, Z_п, e

на min

Нет 9 Да 14

Z_п > Z Останов

Рисунок 3.12 – Алгоритм координатного спирального спуска

Рисунок 3.13 – Графическая интерпретация метода Розенброка

Метод Пауэлла основан на определении направлений поиска путем проведения касательных к изолиниям (изоповерхностям), параллельных друг другу. Линия, соединяющая точки касания определяет текущее направление поиска Z₁. Графическое представление метода приведено на рисунке 3.14.

Рисунок 3.14 – Графическая интерпретация метода Пауэлла

Итерационные процессы оптимизации, в которых направление поиска на каждом шаге совпадает с антиградиентом функции, называются градиентными методами. Отличаются способами выбора величины шагов поиска.

Метод наискорейшего спуска – один из методов с переменным шагом (рисунок 3.15). Шаг выбирается с учетом степени изменения функции в направлении поиска:

H_i = h S_i G_i,

где i – номер переменной; H_i – шаг поиска; h – относительный шаг поиска; S_i – шкальность изменения переменных; G_i – значение антиградиента функции по х_i. Шаг H_i остается постоянным до тех пор, пока значение функции убывает (растет).

Рисунок 3.15 – Графическая интерпретация метода наискорейшего спуска

Шкальность определяется зависимостью S_i = (x_н – x_в)_i b_ш , где x_н, x_в – соответственно принятая нижняя и верхняя граница интервала поиска; b_ш – коэффициент, определяющий шкальность по переменным.

Имеется ряд методов оптимизации на основе случайного поиска. Ниже приведен алгоритм метода случайного поиска с пересчетом. В алгоритме приняты обозначения: r – псевдослучайные числа в интервале от 0 до 1.0; S_i – шкальность изменения x_i; X_т = {x_тi} – текущее значение X; X_п = {x_пi} – текущее приближение к решению X.

Поиск по сайту: