 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оптимизация запасов
!
Рассмотренные ранее методики нормирования запасов ориентированы на использование данных за прошлые периоды и тенденции, сложившиеся в прошлом.
Этот подход дает положительные результаты при незначительных колебаниях запасов в прошлом, но не позволяет ответить на вопросы: оптимален ли запас, является ли его величина наиболее выгодной для предприятия?
В настоящее время существует большое число методов оптимизации запасов. Они различаются степенью сложности, повышая которую можно получить более адекватные и надежные результаты.
Все же приходится признать, что универсальных моделей, способных учесть огромное число факторов, влияющих на величину запасов, не существует. Поэтому на практике стараются применять простейшие модели, позволяющие получить в лучшем случае лишь порядок величины оптимального запаса. Различного рода местные нюансы учитываются путем внесения поправок экспертным путем.
С учетом сказанного, рассмотрим простейшую модель оптимизации производственного запаса, называемую формулой Уил-
сона. С помощью этой формулы определяется такая величина запаса, при которой достигается минимум затрат по его завозу и хранению.
При конструировании модели вводятся дополнительные условия, которые позволяют получить достаточно простую и прозрачную модель. При этом процесс моделирования сохраняет технологию и этапы, присущие разработке "больших моделей".
Условия сводятся к тому, что все партии и интервалы поставок считаются одинаковыми, затраты на выполнение одного заказа не зависят от его величины, затраты по хранению единицы запаса также не зависят от размеров хранимого запаса.
При таких условиях число поставок (N) определяется как частное от деления общего количества запланированного поступления в периоде материалов (М) на объем одной поставки (V).
Расходы на выполнение всех заказов (партий поставки) определяются как произведение стоимости завоза одной партии И1 на число партий (N).
Расходы по хранению текущего запаса в течение всего пла
нируемого периода определяются как произведение среднего те
кущего запаса на стоимость хранения единицы запаса в течение
всего периода. _
Определим средний текущий запас на складе 3 как половину
партии поставки. Последнее станет понятно, если учесть, что к
моменту поступления очередной партии текущий запас равен О,
и все партии одинакового объема. _
Тогда расходы по хранению запаса на складе будут равны И23, где И2 — затраты по хранению единицы запаса в течение периода (квартала, года).

Напомним, что задача сводится к минимизации общих издержек И путем подбора величины партии поставки V.
Эту задачу можно решить, вычислив И по вышеприведенной формуле, придавая V различные значения, от минимального до максимально значения.
Рассмотрим этот процесс на конкретном примере:
Годовой объем поступления (П) — 250 т.
Издержки заказа (H1) — 4,6 усл.ед.
Издержки хранения 1 т в течение года — 2,5 усл.ед.
Построим расчетную табл. 2.8. Таблица 2 8 Зависимость затрат от объема партии поставки

|
В таблице объем партии поставки изменяется от 10 до 80 т с шагом 10 т. Для каждого значения Vi рассчитываются издержки завоза, хранения и их сумма (И1 И2 И) Результаты расчетов отображены на диаграмме (рис. 2.14). Из таблицы видно, что оптимальная (в смысле минимума затрат) партия поставки равна 30 т. Затраты при этом составят 76 усл.ед.

Рис. 2.14. Зависимость издержек от объема партии поставки
Стоит обратить внимание, что вблизи оптимума затраты мало зависят от величины партии, особенно в сторону роста объема поставок. Этим обстоятельством можно воспользоваться для
корректировки партии поставки и этим обеспечить более полную загрузку транспорта, более удобные интервалы поставок и т.п. Особо следует отметить, что если предприятие ощущает недостаток оборотных средств, а это характерно для современных условий, то следует, по возможности, уменьшать величину партии поставки до величины, пока не станут заметно сказываться расходы по завозу.

|
| Дифференцируем функцию по V, приравниваем ее к 0 и решаем относительно V. В результате получим искомую формулу Уилсона: |

|
| Подставим в формулу конкретные данные из примера, получим точное значение величины партии поставки: |

|
Попробуем теперь вывести расчетную формулу, которая позволит непосредственно получать оптимальный объем поставки. Для этого необходимо представить уравнение как функцию:
Как видим, полученная величина согласуется с графиком, что делает излишним использование ранее приведенного пошагового метода непосредственных расчетов оптимальных значений поставок.
Формула Уилсона не получила широкого распространения в практике плановых расчетов, особенно при планировании многономенклатурных запасов ввиду сложности исчисления удельных затрат H1 и И2 при хранении на складах различных материалов.
Кроме того, не следует забывать, что в действительности издержки завоза одной партии И] все-таки зависят от величины партии поставки V, а издержки хранения единицы материала на складе И2 также будут различны при разных объемах хранящихся на складе запасов.
Таким образом, формула Уилсона эффективна при хранении материалов одного вида, незначительных колебаниях партий поставок и величины запасов в течение всего планового периода. Нетрудно обнаружить, что подобные условия могут возникнуть нечасто.
Перечисленные ограничения можно значительно ослабить. Если внимательно посмотреть на приведенную формулу, то
можно увидеть, что вовсе не обязательно вычислять И1 и И2 Достаточно каким-либо образом рассчитать их отношение: И1 / И2. К тому же, приняв, что эта величина для всех материалов, хранящихся на складе, примерно одинакова, можно легко построить модифицированную формулу, не требующую вычисления самих удельных затрат:

|
С другой стороны, партию поставки можно выразить через объем потребления М и число поставок п.
Сделав необходимые преобразования, получим:

Данная формула справедлива для одного материала. По всем материалам, хранящимся на складе, Н* рассчитывается по другой формуле

где Мi — i- и материал; ni, — число поставок в i и партии.
Оптимальный текущий запас в этом случае можно рассчитать по каждому материалу:
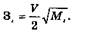
Подобные расчеты проводятся по всем материалам, поступающим на склад, исходя из заключенных договоров на планируемый период.
Рассмотрим на числовом примере порядок оптимизации запаса по нескольким материалам изложенным выше способом.
Как видно из табл. 2.9, до оптимизации фактический запас по трем материалам составлял 53 единицы, при этом выполнено 19 поставок. По этим данным вначале было рассчитано отношение H1 к И2, равное 2,21. Далее были рассчитаны оптимальные партии поставок по всем материалам. Для получения оптимального запаса пришлось бы увеличить число поставок по материалам А и Б при одновременном их уменьшении по материалу В. Благодаря этому, хотя общее число поставок сохранилось, величина оптимального запаса оказалась на 6 единиц меньше фактической.
Попутно отметим, что в данном расчете ставилась задача сократить издержки. Абсолютная величина запаса при этом

|
могла не только не уменьшиться, но, наоборот, возрасти. Экономия затрат при этом была бы достигнута за счет расходов по оформлению заказов.
При оформлении заказов необходимо следить, чтобы величина партии поставок была кратной применяемой таре или упаковке. Как было показано выше, изменение величины запаса в определенных пределах мало сказывается на издержках, если материалы не относятся к дорогостоящим и не отвлекают оборотные средства предприятия.
В БГЭУ на кафедре промышленного маркетинга разработана компьютерная программа "ЗАПАС", с помощью которой эти расчеты можно проводить в автоматизированном режиме при любом количестве материалов, поставляемых на материальный склад предприятия.
Кроме запасов сырья и материалов, практически каждое предприятие имеет запасы узлов, деталей, блоков и для комплектации производимой продукции или ремонта станков и оборудования. В последние годы наметилась устойчивая тенденция роста стоимости комплектующих и запасных частей, что во многом определяется повышенными требованиями к его качеству, а также общим процессом усложнения выпускаемой продукции.
В связи с этим возникает необходимость определения такого комплектного запаса, при котором обеспечивалась бы бесперебойная работа оборудования при минимуме запасных частей. Учитывая, что выход из строя оборудования происходит случайно, в данном случае для определения количества запасных частей нужно применить задачу управления запасами при случайном спросе.
Предположим, что требуются запасные части одного наименования. Вероятность поломки т штук этих деталей обозначим как Р(т). Известны также стоимость одной детали С. и затраты, связанные с ее отсутствием на складе С2. Необходимо определить такое количество запчастей (N), которое сводит к минимуму суммарные затраты на приобретение запчастей и покрытие убытков от их нехватки на складе. При этом могут возникнуть две ситуации: запас перекрывает потребность в замене вышедших из строя запчастей или, наоборот, их имеется недостаточно.
Общие затраты на приобретение и возмещение потерь из-за нехватки запчастей при их поломке можно математически описать следующим образом:


|
| Установим значение этой функции для: |
Последовательно вычисляя левую и правую части неравенства, можно определить такое N, при котором соотношение С1 / (С1 + С2) окажется заключенным между первым и вторым неравенствами. Это значение и является оптимальным.
При массовых поломках мелких деталей на крупных предприятиях с однотипным оборудованием, спрос (поломки) можно считать непрерывной величиной, а распределение вероятностей Рт заменяем на плотность распределения вероятностей fт и получаем следующую математическую модель:

После соответствующих преобразований получаем модель оптимального количества запасных частей:

Как и предыдущая, эта задача также решается на ПЭВМ. Входной информацией для ее решения служат: С1,С2 и Р1 — вероятность выхода из строя первого станка. Например, при С1 = 20 000 р; С2 = 50 000 р., т = 7 и Р1 равном 0,35, 0,22, 0,16, 0,1, 0,08, 0,06, 0,603, оптимальная величина запаса равна четырем изделиям при суммарных затратах, равных 47 500 р.
Очевидно, что для уменьшения потерь необходимо повышать надежность работы оборудования, при этом вероятности выхода, их строй сместятся в сторону меньших величин.
Рассмотренные модели отличаются простой структурой. При этом влияние на величину запасов множества реальных факторов не раскрывается. Кроме того, приводимые расчетные формулы оказываются слишком идеализированными и сглаживают "острые углы", недостаточно учитывают реальные колебания запасов во времени. Вообще есть основание полагать, что прием-
лемого для практических целей аналитического описания динамики запасов в обозримом будущем вряд ли удастся получить.
Значительно лучшие результаты можно получить при использовании для оптимизации запасов метода имитационного моделирования. В данном случае используется метод статистического моделирования, суть которого заключается в следующем.
На первом этапе строится модель, описывающая динамику запасов. Затем собирают и подготавливают конкретные значения факторов, включенных в модель. Далее, изменяя факторы в определенных пределах, получают на выходе соответствующую величину запасов. Заметим, что экспериментатор должен располагать соответствующей компьютерной программой, с помощью которой и проигрывается (имитируется) реальный процесс.
На кафедре промышленного маркетинга разработана и используется программа "Запас", реализующая простейший алгоритм, построенный на известной балансовой формуле Зн + П = Р + Зк. В данном случае моделируется изменение запасов за определенный период времени, например, месяц, квартал, год под влиянием поступления материалов на склад (П) и их реализации, отпуска со склада (Р). При этом исходная балансовая модель решается относительно конечного запаса (Зк): Зк = Зя + П — Р.
Критерием оптимальности служит величина запаса. Цель состоит в том, чтобы определить минимальную величину запаса, при которой еще возможна нормальная, без перебоев, реализация материала.
Очевидно, что моделирование начинается при Зн = 0, т.е. при отсутствии запаса. Методом Монте-Карло разыгрываются значения влияющих факторов П и Р. Их размерность и пределы изменения на моделируемом отрезке времени определяет экспериментатор по результатам анализа реальной ситуации, сложившейся на предприятии за предшествующий период. Конечно, различные аномальные значения факторов в модель не включаются.
Рассмотрим на примере алгоритм работы программы статистического моделирования запасов (табл. 2.10).
Период моделирования здесь равен 7 дням. Условия моделирования: поступление (П) изменяется в пределах от 4 до 8, реализация (Р) — от 3 до 8 единиц материала. Поступление и реализация осуществляются ежедневно. И поступление, и реализация изменяются в соответствии с равномерным законом распределения, т.е. выпадение того или иного конкретного значения П и Р равновероятно.

Напомним, в начале периода значение 30 = О. Пусть при первом розыгрыше выпало П1 = 5, р1 = 4 единицам товара. Тогда: Зк1* =0 + 5 — 4 = 1, т.е. на складе к концу первого дня осталась нереализованной одна единица материала.
При моделировании второго дня ситуация изменилась: П = 4, Р = 6, а Зк2* = 1 + 4-6 = -1. Это означает, что для выполнения заказа не хватает одной единицы материала, что и нашло отражение в графе Зк*.
Алгоритм не допускает дефицита, поэтому единственное решение состоит в том, чтобы предусмотреть его восполнение за счет запаса, а это возможно, если 30 = О + 1 = 1. Тогда Зк1** = 2, а 3К2** = 0.
При моделировании запаса третьего дня дефицит оказывается равным 2, и процесс корректировки 30,31 продолжается (см. столбец Зк***).
В нашем примере все последующие дни не требуют корректировки начального запаса 30.
К концу недели оказалось, что Зк7*** — 0, а средний запас за неделю равен 1,71. Отметим, что это — минимально возможный запас, обеспечивающий выполнение заказов потребителей при сложившихся условиях.
На рис. 2.15 хорошо видно, как запасы обеспечивают необходимое для выполнения заказов соотношение с Р (отпуском товаров со склада). Например, в течение первых трех дней заказы выполнялись частично за счет начального запаса, так как поступление материала было недостаточным.
С другой стороны, казалось, можно снизить запасы 4-го и

5-го дней, но в этом случае заказы 6-го и 7-го дней оказались бы невыполненными.
Для получения практически значимых результатов рассмотренный процесс моделирования многократно повторяется. Для получения научно значимых результатов необходимо выполнить около 70 000 таких повторений, называемых реализациями (не путать с показателем реализации), и усреднить полученные данные. Для получения практически значимых результатов достаточно выполнить 70—100 реализаций.
Имитационное моделирование позволяет строить достаточно сложные модели, близко описывающие реальные процессы. Однако надо иметь в виду, что чрезмерное усложнение моделей потребует больших машинных ресурсов, особенно если моделируются многономенклатурные запасы.
ОБЕСПЕЧЕНИЕ ВЫПОЛНЕНИЯ ПЛАНА МАТЕРИАЛЬНО-ТЕХНИЧЕСКОГО СНАБЖЕНИЯ ПРЕДПРИЯТИЯ
Поиск по сайту: