Прогнозирование потребности предприятия в материальных ресурсах

Планирование потребности в сырье и материалах рассмот­ренными ранее методами требует наличия исходных данных, которые не всегда имеются в момент составления заявки. Кро­ме того, при стабильном потреблении материалов, когда наб­людаются незначительные колебания потребности, нет необхо­димости в подробных расчетах. Достаточно точные результаты можно получить с помощью методов статистического прогно­зирования.

С помощью прогнозов выявляются как положительные тен­денции в их развитии, так и негативные, и принимаются соот­ветствующие меры по устранению недостатков.

Из множества методов прогнозирования в торговых фирмах и на предприятиях получили преимущественное распространение методы экстраполяции, среди которых наибольшее применение находит метод подбора функций. Основная его идея состоит в ис­пользовании факта инерционности экономических процессов. Достаточно выявить основную тенденцию развития явления во времени и ее можно использовать для разработки прогноза.

В общем виде потребность представляется как функция вре­мени:

Наиболее простой функцией является уравнение прямой:

Таким образом, если определить коэффициенты (параметры) а₀ и а,, то потребность Y можно вычислять, подставляя вместо t его конкретные значения (дни, недели, месяцы, годы — в зави­симости от наличия исходных данных).

Параметры а₀ и а₁ должны быть такими, чтобы рассчитан­ный по приведенной функции у в наименьшей степени отлича­лись от их фактических значений в прошлом периоде. Чаще все­го для определения указанных параметров используется метод наименьших квадратов, с помощью которого минимизируется сумма квадратов отклонений, рассчитанных по формуле значе­ний от фактических:

Так как в данной функции переменными являются парамет­ры а₀ и а₁, которые и требуется подобрать так, чтобы обеспечить минимум функции, то по ним находят частные производные и приравнивают их к нулю.

В итоге получается система так называемых нормальных уравнений:

Решая уравнения относительно параметров а₀ и а₁ получаем их искомые значения.

В последующем их подставляют в уравнение регрессии: у = а₀ + a₁t и, придавая t значения прогнозируемых периодов (дней, месяцев, кварталов, лет), получаем прогнозы потребности.

Метод подбора функций предполагает, что всякий раз после получения расчетных значений, они должны быть оценены на близость к фактическим, по которым, собственно, и были рас­считаны.

Наиболее важными показателями близости или точности подгонки можно использовать:

коэффициент детерминации (квадрат коэффициента корре­ляции между у и t:

коэффициент аппроксимации (среднее относительное ли­нейное отклонение абсолютных значений у фактического от у расчетного).

Коэффициент аппроксимации определяется по формуле

Чем меньше этот коэффициент, тем лучшей считается под­гонка у. В практике прогнозирования принято считать достаточ­но высокой оценку К_а, равную 0,1, и удовлетворительной — 0,2.

Использование уравнения прямой для прогнозирования пот­ребности в сырье и материалах далеко не всегда позволяет полу­чить достаточное приближение, вследствие чего приходится ис­пользовать другие виды функций. Для того чтобы иметь воз-

можность применить линейный метод наименьших квадратов для нахождения параметров, надо предварительно линеаризи­ровать функции путем замены исходных данных на их преобра­зованные значения. Например, степенная функция у - a₀t^а1 легко линеаризуется логарифмированием: InY = In a₀ +a₁t. В этом случае минимум суммы квадратов достигается не для ис­ходных значений, а для их логарифмов.

Ниже приводятся наиболее применяемые функции и их пре­образования (табл. 2.6).

Таблица 2.6. Функции и их преобразования

Для прогнозирования могут использоваться и другие фун­кции, однако следует придерживаться правила: выбирать не ту функцию, которая дает наименьший коэффициент аппроксима­ции и наибольшую корреляцию, а ту, которую легче интерпре­тировать в терминах экономики. Например, если экспоненци­альная функция дает коэффициент аппроксимации 0,14, а фун­кция прямой — 0,15, то следует все же использовать для про­гнозирования последнюю.

Особого внимания заслуживают параболические функции, с помощью которых можно получить наибольшее приближение исходных и расчетных данных, если увеличивать степень (поря­док) параболы. Однако опыт применения параболического сгла­живания функций для прогнозирования говорит о том, что и здесь разумно ограничиться параболой второго порядка:

Ее коэффициенты поддаются убедительной интерпретации:

а₁ показывает ежегодный линейный прирост, а₂ — ускоре­ние прироста (если знак отрицательный, то замедления).

Таким образом, задача прогнозирования методом подбора функций сводится к получению и сравнению с фактическими расчетных значений по каждой функции и выбору наиболее приемлемой по принятому критерию.

Экстраполяция по времени не всегда дает положительный результат из-за значительных нелинейностей в исходных дни

ных. В таких случаях иногда можно воспользоваться методом моделирования, применив в качестве факторного признака объ­ем производства:

где х — объем производства.

Параметры модели находят аналогично — методом наимень­ших квадратов. Можно усложнить модель, введя в нее фактор времени:

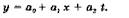
Такая двухфакторная модель может более точно описать из­менение потребности в материальных ценностях за анализируе­мый период, так как здесь учитывается не только объем произ­водства как фактор, непосредственно влияющий на потреб­ность, но и фактор времени, учитывающий временные тенден­ции. Модель можно усложнять и далее. Например, с точки зре­ния удовлетворительной интерпретации результатов, вполне пригодна для прогнозирования такая модель:

Важно помнить, что всякое усложнение модели путем введе­ния в нее новых факторов или их модификации неизбежно сни­жает точность прогноза, требует для получения той же надеж­ности прогноза дополнительных данных (наблюдений), что в по­давляющем большинстве случаев трудно или невозможно осу­ществить. Вообще применение методов прогнозирования требу­ет систематического планового накопления на предприятии фактических данных о поступлении и расходовании материалов за возможно длительный период. Для получения надежного про­гноза необходимо, чтобы число значений исходного ряда превы­шало период прогнозирования, по крайней мере, в 7—10 раз, т.е. для разработки прогноза на один год (квартал) требуется исход­ная информация, по крайней мере, за 10 предшествующих лет (для квартального прогнозирования — кварталов).

Рассмотренные модели прогнозирования (в равной мере) учитывают все включаемые в них исходные данные независимо от времени их представления. Между тем хорошо известно, что временные ряды, состоящие, например, из таких данных, как объем реализации, потребности в материалах, по мере старения теряют свою информационную ценность. Для прогнозирования важнее знать потребность, например, прошлого года, чем позап­рошлого, т.е. по мере удаления от настоящего желательно вклю­чать информацию с меньшим весом. Поэтому для прогнозирова­ния потребности можно с успехом применять метод экспоненци-

ального сглаживания, который обеспечивает не только сглажи­вание (устранение случайных колебаний исходных данных), но и позволяет включать данные с весом, убывающим по мере их старения. Убывание веса данных по мере их старения происхо­дит по экспоненте, что и отражено в названии метода. Основная формула сглаживания:

где S^k_t — сглаженное значение k-ro порядка; а и B — параметры сгла­живания; t — период, к которому относится сглаженное значение.

Как видно из формулы, чтобы сгладить ряд данных, необхо­димо иметь сглаженные значения предыдущего порядка за пре­дыдущий период, с какого бы периода мы не начали сглажива­ние. В качестве сглаженных данных нулевого порядка прини­маем исходный ряд, тогда формула для получения сглаженных значений первого порядка будет иметь вид:

Здесь вновь сталкиваемся с проблемой сглаженного значе-ния за предыдущий S_ti период. Имеется ряд методов получения этого значения для процедуры сглаживания. Можно, например, в качестве сглаженного значения взять среднее арифметичес­кое, вычисленное по 3—4 значениям исходного ряда:

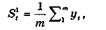
где т должно быть не менее 3-х и в то же время составлять не более 20 % от числа значений исходного ряда.

Предпочтительнее, однако, вычислить его рассмотренным ранее методом наименьших квадратов, т.е. функции прямой или параболы. Важное значение для процедуры сглаживания имеет выбор коэффициентов (параметров сглаживания) а и B. По условию а + B = 1, поэтому практически определяется a, a B вычисляется по формуле.

Для нахождения параметра сглаживания разработано не­сколько методов, например, предлагается простая формула

Из этой формулы видно, что с увеличением длины ряда ис­ходных данных п, а уменьшается, а это означает, что более ста­рые данные приобретают больший вес. Для экономических про­гнозов предпочитают использовать параметр сглаживания, рав­ный не менее 0,1, а это значит, что ряды, длиннее 20 значений, сглаживать при таком а не имеет смысла. На кафедре промыш-

ленного маркетинга разработан учебный пакет программ REG52 по прогнозированию. В нем используется итеративная процеду­ра нахождения оптимального параметра сглаживания.

Начиная с некоторого минимального значения, например, а₁= 0,01, производится сглаживание: S_t^k = a S_t^k-1 + B S_t1^k, нахо­дятся расчетные значения y_t. Они сравниваются с фактически­ми значениями, т.е. вычисляется сумма квадратов отклонений расчетных значений от фактических. Затем прибавляется при­ращение а_r = а_r+ 0,001, и весь процесс повторяется до тех пор, пока будет уменьшаться сумма квадратов отклонений SS_r Ми­нимальной сумме квадратов отклонений расчетных значений от фактических соответствует оптимальное значение а_г.

Найденное таким образом оптимальное значение параметра сглаживания используется для прогнозирования. Имея сгла­женные значения первых 3-х порядков, можно получить про­гнозы по линейной и квадратичной моделям.

Для этого рассчитываются а параметры для подстановки в соответствующие формулы.

Пример прогнозирования методом экспоненциального сгла­живания на небольшом отрезке, включающем всего 5 значений потребности в материале, приведен в табл. 2.7.

В данном примере параметр сглаживания определен по фор­муле

В качестве S₀ принято первое значение исходного ряда (69 т). Тем самым это значение потеряно как самостоятельный исход­ный член ряда, поэтому определим первые три сглаженные зна­чения для t = 2:

Для квадратической функции у = а₀+ а₁ t + 0,5 a₂t² рассчиты­ваем параметры а₀ а₁ а₂. Следует обратить внимание, что здесь па­раметры а рассчитываются для каждого периода, пока не будет получено их значение для последнего периода. Именно эти послед­ние значения используются для прогнозирования.

В данном случае значение t для прогнозирования определя­ется по формуле t = t + 1, где t — период прогнозирования.

Ошибка, допущенная при прогнозировании, рассчитывается по формуле

где б_e — среднеквадратическое отклонение расчетных значении от фактических (среднеквадратическая ошибка расчета).

В нашем случае б_Е = 0,75, следовательно, б _у — 1,35, т.е. прогнозируемое значение у₆ окажется в интервале от 81,7 до 84,6 т. Такая точность для большинства практических расчетов оказывается вполне приемлемой.

Рассмотренный пример показывает, что применение методов прогнозирования связано с громоздкими расчетами, которые целесообразно проводить с помощью учебного пакета программ REG 52 (программа EXPOW, БГЭУ, кафедра промышленного маркетинга) для линейной и квадратической модели. Имеющи­еся в распечатке оценки ошибок прогнозирования позволяют судить о надежности и точности прогноза и выбрать наилучший метод прогнозирования в каждом конкретном случае.

Входной информацией для этой программы служит исход­ный ряд (или несколько рядов) с указанием числа наблюдений (периодов ретроспективы) и периода прогнозирования.

Содержание, функции и состав производственных запасов

Поиск по сайту: