 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Транспортная задача линейного программирования
Ряд задач оперативного управления сводятся к решению задачи оптимального закрепления потребителей за поставщиками, состоящей в определении наилучшего плана поставок однородных (взаимозаменяемых) ресурсов (грузов, автомобилей и т.п.) от m поставщиков Ai ( ) к n потребителям Bj (
) к n потребителям Bj (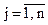 ). Такой план должен обеспечивать соблюдение ограничений по наличию и потребностям ресурсов, а также минимальные транспортные издержки. Вместо стоимости при поиске оптимальных решений могут приниматься за основу расстояния поставки, время на движение, условные расстояния и другие показатели. Наиболее часто применяются расстояния перевозки.
). Такой план должен обеспечивать соблюдение ограничений по наличию и потребностям ресурсов, а также минимальные транспортные издержки. Вместо стоимости при поиске оптимальных решений могут приниматься за основу расстояния поставки, время на движение, условные расстояния и другие показатели. Наиболее часто применяются расстояния перевозки.
Задача оптимизации закрепления потребителей за поставщиками применяется при оптимизации грузопотоков (грузоотправители – поставщики, грузополучатели – потребители), возврата порожних транспортных средств (грузополучатели – поставщики порожних транспортных средств, грузоотправители – получатели порожних транспортных средств), подачи транспортных средств в начальные пункты маршрутов (предприятия-перевозчики – поставщики, начальные пункты маршрутов – получатели транспортных средств). Первая задача – получить грузопотоки, обеспечивающие минимальный грузооборот; вторая и третья – обеспечить минимум непроизводительных перемещений транспортных средств.
На основании полученных оптимальных планов закрепления потребителей ресурса за поставщиками может строиться картограмма поставок. Для этого эпюры потоков ресурса накладываются на схему транспортной сети. При построении необходимо учитывать, что ресурс корреспондирует по пути с минимальной стоимостью перемещения (кратчайшему пути) между пунктами i и j транспортной сети.
Если обозначить размер ресурса (вывоза) от поставщика Ai через XAi, требуемый размер поставки потребителю Bj через XBj, размер корреспонденции от i-го поставщика j-му получателю (потребителю) через Xij и стоимость поставки единицы ресурса между ними через lij, то поставленная задача в математической форме примет вид:
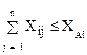 ; (3.1)
; (3.1)
 (3.2)
(3.2)
 ; (3.3)
; (3.3)
Xij ³ 0. (3.4)
В случае, если запасы у поставщиков равны общим потребностям получателей, то
 . (3.5)
. (3.5)
Поставленная таким образом задача (ограничения 3.1, 3.2, 3.4 и целевая функция 3.3) является сбалансированной моделью (условие 3.5) классической транспортной задачи линейного программирования, в результате решения которой по известным значениям XAi, XBj, lij находятся оптимальные значения корреспонденций Xij.
Задача может быть поставлена с дополнительными условиями:
1) имеются ограничения на размер поставок от каждого i-го поставщика каждому j-му потребителю в объемах Xоij,  ;
; 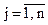 ;
;
2) запрещена поставка ресурса от i-го поставщика j-му потребителю, т.е. должно быть обеспечено условие Xij=0;
3) должна быть обеспечена поставка от i-го поставщика j-му потребителю в гарантированном объеме Xгij (Xгij ≤ XАi и Xгij ≤ XВj );
4) при несбалансированной задаче необходимо назначить по какому-то из пунктов корреспонденцию реального или фиктивного ресурса.
Для решения транспортная задача может быть представлена в виде распределительной таблицы (таблица 3.23).
Общий алгоритм решения несбалансированной задачи с учетом ограничений на размер корреспонденций представлен на рисунке 3.23.
Приведение несбалансированной задачи к сбалансированному виду производится по алгоритму:
1) рассчитываются суммарный объем наличия ресурса XсА и суммарный объем потребности в ресурсе XсВ
 ;
;
 ;
;
2) сравниваются объемы XсА и XсВ. Если они равны, то задача сбалансирована, иначе на пункт 3;
3) если XсА > XсВ, то вводится фиктивный потребитель (n=n+1) и если XсА<XсВ –фиктивный поставщик (m=m+1);
4) по фиктивному потребителю или поставщику назначается объем ресурса в размере abs(XсА - XсВ);
5) назначаются стоимости по фиктивному пункту равными постоянной величине, например lф=  (для фиктивного потребителя lin = lф ,
(для фиктивного потребителя lin = lф ,  или для фиктивного поcтавщика lmj =lф ,
или для фиктивного поcтавщика lmj =lф , 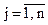 ;
;
6) назначаются ограничения по фиктивному пункту, равными постоянной величине, например Xoф ³abs(XсА-XсВ) (для фиктивного потребителя Xoij = Xoф, j=n,  или для поставщика Xoij = Xoф , i=m,
или для поставщика Xoij = Xoф , i=m, 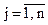 ).
).
Для отыскания оптимального закрепления потребителей за поставщиками необходимо сделать в распределительной таблице первоначальное закрепление, т.е. получить произвольный план закрепления (опорный), удовлетворяющий ограничениям (3.1), (3.2), (3.4) и (3.5) при числе загруженных связей m+n-1 и отсутствии циклов (контуров). План, содержащий ровно m+n-1 загруженных связей без циклов, называется базисным.
 1
1
Ввод исходных данных: число и
название пунктов, объемы запасов
и потребностей ресурса, стоимос-
ти возможных поставок на едини-
цу ресурса, ограничения на
размер корреспонденций 3
Введение фиктивного поставщика
(потребителя), объема ресурса по
2 Нет нему, условных стоимостей пос-
Наличие баланса? тавок и ограничений
Да
Составление первоначального ба-
зисного плана поставок ресурса
(с учетом стоимостей)
5 Да Нет 6 Имеются
План оптимален? ли ограничения на размер
корреспонденций?
Нет Да
7 8
Улучшение плана поcтавок Ввод в окончательное решение
путем их перераспределения поставок в размере ограничений
по определенному правилу (где превышены), корректировка
ограничений и стоимостей
9 Размер поставок Да
превышает
ограничения?
Нет
11 10
Вывод результата решения: Формирование окончательного
название корреспондирующих решения: последнее
пунктов, размер и стоимость распределение и ранее
поставок ресурса включенные в него поставки
Рисунок 3.23 – Укрупненный алгоритм решения транспортной задачи линейного программирования
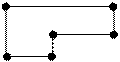
Цикл (контур) в распределительной таблице – это условная замкнутая ломаная линия, образованная прямыми отрезками, углы между которыми равны 90о, а вершины углов лежат в загруженных связях. Контур может быть четырехугольным, шестиугольным, восьмиугольным и т.д. Если число загруженных связей более m+n-1, то среди них есть цикл. Примеры циклов приведены ниже (точками показаны загруженные связи):
 | |||||
 |  | ||||
Существует несколько методов получения опорного плана – метод северо-западного угла (диагональный) и ряд эффективных, дающих решение более близкое к оптимальному,– метод минимального элемента, метод абсолютного двойного предпочтения, метод Фогеля (наиболее эффективный) и др.
Таблица 3.3 – Распределительная таблица (общий вид)
| Поставщи- ки Ai | Потребители Bj | Запас ресурса | Вспомо- гательный | ||||
| B1 | ... | Bj | ... | B n | XAi | Столбец | |
| A1 | |||||||
| ... | ... | ... | ... | ... | ... | ... | ... |
| Ai | sij lij Xij Xоij | Xi | uAi | ||||
| ... | ... | ... | ... | ... | ... | ... | ... |
| Am | |||||||
| Потребность в ресурсе XBj | |||||||
| Вспомогатель-ная строка | uBj |
Для получения первоначального базисного решения рассмотрим применение метода минимального элемента. В соответствии с этим методом распределение составляется по следующему алгоритму:
1) формируются дополнительные массивы стоимостей l'ij (l'ij = l ij), объемов ресурса X'Ai (X'Ai=XAi) и X'Bj (X'Bj =XBj),  ;
; 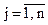 ;
;
2) находится минимальная стоимость из всех связей
 .
.
Если lrw = ¥, то первоначальное базисное решение получено. Иначе на 3);
3) связь rw, соответствующую минимальной стоимости, загружают корреспонденцией Xrw. Объем корреспонденции Xrw , назначаемый для связи rw, определяется как минимум от объемов запаса и потребности с учетом ранее назначенных других поставок:
Xrw = min (X'Ar,X'Bw),
где X'Ar – количество ресурса r-го поставщика с учетом ранее назначенных корреспонденций другим, кроме w-го, потребителям; X'Bw – количество ресурса, требуемого w-му потребителю с учетом ранее назначенных корреспонденций от других, кроме r-го поставщика;
4) из сравниваемых величин X'Ar и X'Bw вычитается значение Xrw , в результате чего получаются измененные ограничения X'Ar =X'Ar - Xrw и X'Bw =X'Bw - Xrw ;
5) изменяется массив l'ij по следующему правилу:
если X'Bw=0, то l'iw = ¥ ( ),
),
иначе (X'Ar=0) l'rj = ¥ (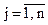 );
);
6) переход на пункт 2).
Пункт 5 алгоритма обеспечивает исключение из дальнейшего рассмотрения поставщика (если X'Ar =0), либо получателя (если X'Bw=0). Остаток объема ресурса X'Ar или X'Bw к дальнейшему распределению может иметь значение, равное нулю.
Полученное таким образом закрепление потребителей ресурса за поставщиками является одним из возможных базисных распределений.
Для оценки оптимальности текущего решения закрепления потребителей ресурса за поставщиками применяется ряд методов: распределительные методы (метод Хичкока, метод Креко, метод МОДИ), методы с разрешающими элементами (метод разрешающих слагаемых и метод разрешающих множителей) и др.
Наиболее широкое применение получил модифицированный метод (МОДИ). В распределительную таблицу вводят вспомогательные строку и столбец; в них вносят специальные показатели, называемые потенциалами. Распределительные методы основаны на следующем: если к стоимостям любой строки (столбца) распределительной таблицы прибавить (или отнять) одно и то же произвольное число, то оценка оптимальности относительно не изменится. Если, например, от стоимостей каждого i-го поставщика отнять число uAi , а от стоимостей каждого j-го потребителя – uBj, то относительной оценкой любой связи ij может служить оценочный параметр sij (вместо l ij):
sij = lij - uAi- uBj. (3.6)
Принимая для загруженных связей sij = 0 и используя выражение (3.6), определяются потенциалы uAi и uBj по следующему правилу:
потенциал для одного пункта, например первого поставщика принимается равным нулю;
по расстояниям загруженных связей подбираются потенциалы для других поставщиков и потребителей таким образом, чтобы соблюдалось принятое условие lij - uAi- uBj = 0, т.е. стоимость для каждой загруженной связи должна быть равна сумме потенциалов по поставщику и потребителю.
Затем по вычисленным потенциалам uAi , uBj определяется, используя формулу (3.6), значение оценочного параметра sij для каждой незагруженной связи (не входящей в базисный план). Величина параметра sij характеризует общее изменение целевой функции, получаемое при включении в план единичной корреспонденции для связи ij по сравнению с рассматриваемым планом.
Если значение оценочного параметра свободной связи будет меньше нуля (sij <0), то это значит, что перераспределение корреспонденций с загрузкой такой связи, называемой потенциальной, уменьшит значение целевой функции на величину abs(sijXij), Xij – размер корреспонденции, которой будет загружена связь ij. Отсутствие связей со значением параметра sij <0 означает, что проверяемый план закрепления потребителей за поставщиками является оптимальным. Если для какой-то свободной связи значение sij равно нулю, то это означает, что можно получить другой план с тем же минимальным значением целевой функции.
Если решение не оптимально, то из всего множества свободных связей выявляется наиболее потенциальная с минимальным значением sij. Загрузка корреспонденцией такой связи дает наибольшее уменьшение целевой функции на каждую единицу перераспределенного объема ресурса.
При перераспределении загрузок по связям в распределительной таблице для наиболее потенциальной связи, как для загруженной, строится контур. Введение к m+n-1 загруженным связям еще одной образует ровно один определенный контур, присущий вводимой связи. После чего связи, соответствующие вершинам контура, нумеруются: номер 1 присваивается выбранной потенциальной связи, а дальнейшая нумерация ведется в порядке следования вершин по контуру (могут присваиваться связям контура положительные и отрицательные знаки).
Затем производится перераспределение по контуру корреспонденций следующим образом:
1) выявляется связь с четным номером, которой соответствует наименьшее значение корреспонденции Xм ;
2) значение объема ресурса Xм вычитается от значений объемов корреспонденций всех связей с четными номерами вершин. Если среди связей с четными номерами вершин окажутся две (или более) с одинаковой минимальной корреспонденцией, то из плана исключается только одна из них, для связи с большим расстоянием поставки, а вместо остальных оставляют условную корреспонденцию с нулевым значением, чтобы не допустить вырождения;
3) для всех связей с нечетными номерами вершин (включая и потенциальную) к значениям объемов корреспонденций прибавляется величина Xм.
В результате одна связь становится свободной, а наиболее потенциальная – получает загрузку. Измененные значения корреспонденций и значения объемов корреспонденций для связей, которые не входили в контур, переносятся в таблицу нового улучшенного плана закрепления потребителей за поставщиками.
Полученный новый план проверяется на оптимальность. Действия по проверке на оптимальность и улучшению распределения повторяются до тех пор, пока не будет найден оптимальный план закрепления потребителей за поставщиками.
При решении транспортной задачи линейного программирования на основе существующего базисного решения возможны варианты, когда число загруженных связей в таблице меньше m+n-1 (случай вырождения) или больше m+n-1 (случай наличия циклов). В первом случае нельзя оценить оптимальность решения, так как невозможно определить потенциалы для некоторых поставщиков и (или) потребителей, во втором – потенциалы определяются неоднозначно.
В случае вырождения необходимое число свободных связей загружают нулями с соблюдением правила: нулевые объемы поставок заносятся для связи поставщиков (потребителей), для которых нельзя рассчитать потенциал, с поставщиками (потребителями), для которых потенциалы уже определены. Целесообразно выбрать из данных связей такие, которым соответствуют наименьшие стоимости поставок. Связи, загруженные нулями, не должны образовывать контуров (циклов) с другими загруженными связями.
В случае наличия циклов для некоторых связей исключают корреспонденции по следующему алгоритму:
1) строится один из возможных контуров;
2) нумеруются углы контура;
3) определяется сумма стоимостей поставок для связей, в которых лежат углы контура с четными номерами и затем с нечетными номерами;
4) среди связей (с четными или нечетными номерами), для которых сумма стоимостей перевозок больше, выявляется связь с наименьшим значением размера корреспонденции Xм;
5) размер корреспонденции Xм вычитается от загрузки каждой из связей с четными или нечетными номерами, для которых сумма стоимостей поставок больше, и прибавляется к загрузке каждой из связей с нечетными или четными номерами, для которых сумма стоимостей поставок меньше.
Указанные действия повторяются до полного исключения циклов (контуров) в распределительной таблице. При этом нельзя допускать вырождения за счет одновременного исключения загрузок для нескольких связей одного цикла. Исключение контуров в распределительной таблице по вышеописанной методике уменьшает одновременно и значение целевой функции.
При отсутствии дополнительных условий полученное оптимальное решение является окончательным.
При наличии ограничений на размер корреспонденций, задача в дальнейшем решается по следующей схеме:
1) проверяется выполнение условия Xij £Xoij для связей ij. Если условие выполняется для всех связей, то решение закончено (переход на блок 10 общего алгоритма), иначе переход на пункт 2;
2) для каждой связи ij, по которой имеет место условие Xij > Xoij , последовательно должен быть реализован алгоритм:
2.1) в окончательное решение вводится корреспонденция Xij = Xoij ;
2.2) корректируются соответствующие размеры наличия и потребности в ресурсе
XА j =XА j - Xij ;
XBj = XBj - Xij ;
2.3) корректируется соответствующая стоимость поставки lij путем замены на большое число, например 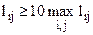 ;
;
3) переход на блок 4 укрупненного алгоритма решения задачи.
Решение задачи с запрещением поставки ресурса от i-го поставщика j-му потребителю решается по общей схеме с предварительной заменой реальной стоимости lij на большое число, например 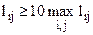 . Тем самым обеспечивается Xij =0.
. Тем самым обеспечивается Xij =0.
Решение задачи с необходимостью обеспечения поставки от i-го поставщика j-му потребителю в гарантированном объеме Xгij производится следующим образом:
1) предварительно для каждой такой связи ij, по которой имеет место условие Xij³Xгij:
1.1) в окончательное решение вводится корреспонденция Xij=Xгij;
1.2) корректируются соответствующие размеры наличия и потребности в ресурсе
XАj=XАj-Xij; XBj=XBj-Xij;
2) решается задача с новыми условиями по общей схеме.
Полное окончательное решение будет представлять собой множество корреспонденций, полученных решением по измененным условиям, и корреспонденций, назначенных по пункту 1.1).
При решении несбалансированной транспортной задачи возможно за счет назначения различных стоимостей по фиктивному пункту распределение по какому-то из пунктов корреспонденции реального или фиктивного ресурса. Так, если по одному из пунктов в корреспонденции с фиктивным поставить относительно большее значение стоимости, то это явится предпосылкой, что по нему будет назначена корреспонденция только реального ресурса (по пункту будет обеспечена поставка реального ресурса). Наоборот, если поставить относительно меньшее значение стоимости, то это вызовет назначение корреспонденции в виде фиктивного ресурса (не будет обеспечена поставка реального ресурса). При одинаковом значении стоимости в корреспонденции с фиктивным пунктом фиктивные поставки будут назначены исходя из минимума общих затрат на поставки, что не всегда отвечает реальным требованиям производства.
Компьютерная программа решения транспортной задачи линейного программирования приведена в приложении 8. Программа состоит из головного модуля, модуля ввода данных и модуля выполнения расчетов.
Пример. На предприятиях Ai пассажирского транспорта имеется следующее число XAi транспортных средств для работы на маршрутах: A1 – XA1 =10; A2 – XA2 =30; A3 – XA3 =40. Для работы на маршрутах Bj требуется следующее число транспортных средств: B1 – XB1 =10; B2 – XB2 =10; B3 – XB3 =20; B4 – XB4 =30. Имеются дополнительные условия:
1) заданы ограничения на размер корреспонденций для всех связей (кроме А1В3) – в размере 30 ед, для А1В3 – в размере 5 ед.;
2) транспортные средства 2-го предприятия необходимо использовать в полном объеме;
3) поставка транспортных средств 2-го предприятия на 2-й маршрут должна быть не менее 5 единиц;
4) поставка транспортных средств 1-го предприятия на 4-й маршрут запрещена.
Требуется оптимальным образом распределить транспортные средства по маршрутам перевозок. Расстояния между предприятиями и маршрутами (нулевые пробеги транспортных средств) приведены ниже в таблице 3.4.
Таблица 3.4 – Данные по нулевым пробегам транспортных средств
Поиск по сайту: