На минимум. Метод золотого сечения основан на делении отрезка [a, b] по правилу золотого сечения, когда отношение большего отрезка к меньшему const

8 Да

Z₁< Z₂

Нет

9 10

a = x_c b = x_c Рисунок 3.3. Схема алгоритма программы по

методу дихотомии

Метод золотого сечения основан на делении отрезка [a, b] по правилу золотого сечения, когда отношение большего отрезка к меньшему const. Такое отношение определяется выражением (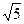 -1)/2=0.62. При этом методе в отличие от метода дихотомии на каждой итерации требуется расчет только одного значения целевой функции. В результате находится решение x_п и соответствующее ему значение целевой функции Z_п (рисунки 3.4, 3.5).

На минимум:

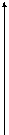f(x)

f(x₂)

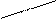(1-k)(b-a)

f(x₁) k(b-a)

a x₁ x₂ b x

Рисунок 3.4 – Графическая интепретация метода золотого сечения

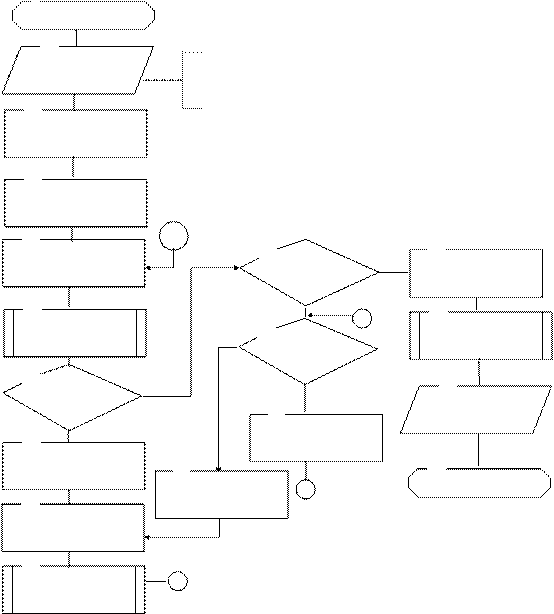1

Пуск

Ввод a, b, e a и b – текущие значения нижней и верхней

границ интервала поиска экстремума

e – точность поиска

k= ( -1)/2

i = 1

5 13

11 Да 15

x₁ = a +(1-k)(b-a) abs(x₂-x₁)<e x_п = (x₂+x₁)/2

6 Нет 16

Z₁ = f(x₁) на минимум 10

Нет 12 Z_п = f(x_п)

Z₁ < Z₂

Нет Да 17

i=1 13 Вывод x_п , Z_п

8 Да b= x₂: x₂ = x₁

Z₂ = Z₁

i = 1 14 18

a= x₁: x_{1 -}= x₂ 5 Останов

9 Z_1-= Z₂

x₂ = a + k (b-a)

Z₂ = f(x₂) 12

Рисунок 3.5. Схема алгоритма программы по методу

золотого сечения

Метод Фибоначчи основан на делении отрезка [a, b] с использованием чисел Фибоначчи, представляющих ряд, у которого последующее число равно сумме двух предыдущих (1,1,2,3,5,8 и т.д.).

Шаговые методы основаны на том, что текущему приближению к решению x_п на каждом новом шаге дается приращение h как x_п=x_п+h и вычисляется f(x_п). Если новое значение целевой функции "лучше" предыдущего, то переменной x дается новое приращение. Если функция "ухудшилась", то поиск в данном направлении завершен.

Имеется ряд разновидностей шагового метода поиска экстремума целевых функций (прямой поиск, поразрядного приближения, Зейделя и др.).

Графическая интепретация и алгоритм поиска экстремума функции на основе поразрядного приближения приведены на рисунках 3.6, 3.7.

f(x)

f(x_п+h)

f(x_п) На минимум

x_п x_п+h x

Рисунок 3.6 – Графическая интепретация метода поразрядного приближения

1

Пуск

x_п, h, a,e x_п и h – текущие значения соответственно приближения

к решению и шага поиска; a – коэффициент

изменения шага поиска; e – точность поиска решения

Z = f(x_п)

Z_п = Z

x_п = x_п + h

Z= f(x_п)

Поиск по сайту: