Водородоподобные атомы. Энергетические уровни. Квантовые числа

Ответ: Как следует из соотношений, полученных при решении задачи 5.1, длина волны де Бройля для движущегося в атоме электрона сравнима с размером атома. Мы знаем, что в этих условиях нельзя пренебречь волновыми свойствами электрона, и его движение в атоме не может быть описано законами классической физики. Поэтому атомные системы являются важнейшими объектами физики, для описания которых следует обязательно использовать законы квантовой механики. При этом существенно, что для такого описания квантовая механика не требует каких-либо дополнительных предположений, условий и постулатов, аналогичных постулатам в теории Бора. Сформулируем постановку стационарной задачи квантовой механики для водородоподобного атома, описывающей движение электрона в электрическом поле неподвижного ядра с зарядом , где для атома водорода и для других водородоподобных атомов (ионов). Такая модель является важнейшей моделью атомной физики. Для этой модели потенциал поля, в котором движется электрон, может быть записан точно. Поэтому все выводы квантовой теории водородоподобных атомов могут быть проверены непосредственно в эксперименте. Потенциальная энергия электрона в электрическом поле ядра определяется выражением:

.

(5.16)

Движение электрона в таком поле можно рассматривать как движение в некоторой сферической потенциальной яме, форма которой изображена на рис. 5.6. По аналогии с задачей о движении частицы в потенциальной яме простой формы, рассмотренной в разделе 4.2, можно ожидать, что спектр энергии электрона в атоме будет дискретным, то есть состоять из отдельных энергетических уровней со значениями полной энергии электрона , , 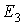и т.д. Для атома водорода этот энергетический спектр должен совпасть с полученным в теории Бора спектром энергий (5.12), который подтверждается в оптических экспериментах.

Рис. 5.6.

Итак, для описания возможных квантовых состояний электрона в водородоподобном атоме и нахождение спектра полной энергии электрона в этих состояниях необходимо найти регулярные решения стационарного уравнения Шредингера:

(5.17)

с гамильтонианом:

.

(5.17a)

Здесь - масса электрона, а - его полная энергия в квантовом состоянии, описываемом волновой функцией . При этом оператор потенциальной энергии есть оператор умножения на функцию , заданную соотношением (5.16). Искомые решения уравнения Шредингера (5.17) являются собственными функциями оператора полной энергии , и их нахождение связано с решением достаточно сложного дифференциального уравнения. Учитывая, что эта задача является одной из важных задач квантовой физики, изложим схему нахождения таких решений достаточно подробно. При изложении этой схемы нам придется использовать специальные функции математической физики - сферические функции. Для некоторых конкретных квантовых состояний они будут выписаны в точной аналитической форме как комбинации известных элементарных функций. Более подробные сведения о свойствах сферических (шаровых) функций можно найти в справочной математической литературе.

Движение электрона в атоме удобнее исследовать, вводя сферическую систему координат, центр которой совпадает с центром ядра атома. В такой системе координат волновая функция электрона имеет вид 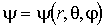, а оператор Лапласа: можно определить как оператор, содержащий радиальную часть:

(5.18)

и угловую часть:

.

(5.19)

Согласно формулам (3.32), оператор квадрата момента импульса в сферической системе координат определяется как . Поэтому уравнение Шредингера (5.17) преобразуется к виду:

.

(5.20)

Решение этого уравнения будем искать в виде произведения двух функций:

(5.21)

с разделяющимися переменными. Оператор коммутирует с гамильтонианом . Поэтому согласно общим положениям квантовой механики, изложенным в главе 3, атом в любом квантовом состоянии должен обладать определенным значением модуля момента импульса, а функция 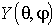должна быть собственной функцией оператора , то есть удовлетворять уравнению:

.

(5.22)

Функции называются сферическими или шаровыми функциями. Эти функции определяются заданием двух целочисленных параметров 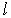и , которые называют квантовыми числами. Орбитальное (азимутальное) квантовое число 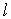принимает значения . Квантовое число называют магнитным квантовым числом. Физический смысл этих квантовых чисел и их названий мы обсудим ниже. Приведем явные формулы для некоторых нормированных сферических функций:

;

;

.

Подставив в (5.20) волновую функцию в форме (5.21), где 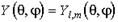, и разделив на этот угловой множитель, получаем уравнение для радиальной функции :

.

(5.23)

Решение этого уравнения будем искать в виде:

.

(5.24)

Тогда подставляя искомую функцию такого вида в уравнение (5.23), получим более простое по форме уравнение для функции :

.

(5.25)

Перейдем в этом уравнении к безразмерным величинам:

,

(5.26)

выбрав в качестве характерного размера боровский радиус: , а в качестве характерной энергии - энергию ионизации атома водорода, найденную в теории Бора: . Тогда уравнение (5.25) примет вид:

.

(5.27)

Точное решение этого дифференциального уравнения с переменными коэффициентами следует искать в виде произведения двух функций:

.

(5.28)

Подставляя (5.28) в (5.27), находим уравнение для новой искомой функции . После несложных вычислений получаем:

.

(5.29)

Функцию , являющуюся решением этого уравнения, будем искать в виде степенного ряда:

.

(5.30)

Для нахождения коэффициентов этого ряда подставим (5.30) в (5.29) и соберем члены ряда с одинаковой степенью . Такая подстановка дает:

.

(5.31)

В первой сумме при 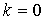выражение в квадратных скобках обращается в нуль. Поэтому суммирование в ней, фактически начинается с . Следовательно, сдвинув на единицу индекс суммирования в первой сумме, формулу (5.31) можно преобразовать к виду: . Чтобы это равенство выполнялось при всех , коэффициент при каждой степени должен быть равным нулю. Поэтому ряд в (5.30) будет решением уравнения (5.29), если выполняется следующее рекуррентное соотношение для его коэффициентов:

.

(5.32)

Однородность уравнения (5.29) позволяет, выбрав значение коэффициента 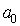, по формуле (5.32) определить , затем найти и т.д. Вычисляя таким образом все коэффициенты , находим искомое решение уравнения (5.29) в виде ряда (5.30) по степеням с известными коэффициентами. Из (5.32) следует, что для достаточно больших значений связь между коэффициентами ряда (5.30) имеет вид . Но именно такая связь существует между коэффициентами ряда: , представляющего разложение экспоненты с показателем степени 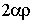. Следовательно, если ряд в (5.30) имеет бесконечное число слагаемых, то для достаточно больших значений функция будет иметь следующую ассимптотику: 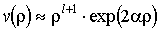. Но тогда из (5.28) следует, что даже после умножения на радиальная составляющая будет неограниченно возрастать при 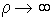. С учетом (5.21) и (5.24) такой же неограниченный рост на бесконечности будет наблюдаться и у искомого решения уравнения Шредингера. Такая функция не удовлетворяет условию нормировки и, следовательно, не может рассматриваться как волновая функция электрона. Однако, построенное решение уравнения Шредингера будет убывать при и удовлетворять всем условиям регулярности, если ряд в (5.30) оборвется на каком либо конечном члене, то есть будет многочленом конечной степени. Только в этом случае экспоненциальный множитель в (5.28) обеспечит убывание квадрата модуля волновой функции на бесконечности. Из (5.32) следует, что обрыв ряда в (5.30) на номере произойдет, если выполнится следующее условие:

.

(5.33)

Обозначим целое число , назвав радиальным квантовым числом, а - главным квантовым числом. Очевидно, что , т. е. . Условие (5.33) в этом случае принимает вид или . С учетом соотношений (5.26), это условие можно сформулировать как условие квантования полной энергии электрона в атоме:

.

(5.34)

Итак, условие регулярности волновой функции привело к условию квантования энергии атома, которое при точно совпало с условием квантования энергии (5.12) в теории Бора. Поэтому из(5.34) также следует экспериментально проверенная формула Бальмера (5.14). Таким образом, радиальная часть волновой функции электрона в водородоподобном атоме зависит от двух квантовых чисел и 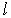и может быть записана в виде:

,

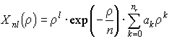(5.35)

где , , причем 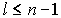, а коэффициенты для находятся из рекуррентных соотношений (5.32). Значение коэффициента 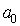, в конечном итоге, выбирается из условия нормировки волновой функции, которое в сферической системе координат запишется в виде:

.

(5.36)

Здесь - элемент объема в сферических координатах. Таким образом, волновая функция, определяющая квантовое состояние электрона в атоме, найдена. Она имеет вид: 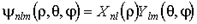и зависит от трех квантовых чисел , 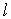и . Для обозначения квантовых состояний с заданным значением орбитального квантового числа 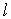используют следующие спектроскопические символы:

Значение					...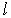
Символ состояния					...

Далее идут , и следующие по латинскому алфавиту буквы состояний. В частности, состояние с называется -состоянием, а электрон в таком состоянии -электроном. Состояние с называется -состоянием и т.д. Для более полного обозначения квантового состояния электрона необходимо указать также значение главного квантового числа . Оно указывается перед символом состояния. Так, электрон в квантовом состоянии с и обозначается символом , в состоянии с и - символом и т.д. Поскольку всегда 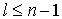, то возможны следующие состояния электрона:

; и т.д. Анализ свойств сферических функций показывает, что все -состояния электрона, то есть состояния с и , являются сферически симметричными состояниями. Волновая функция в этих состояниях не зависит от угловых переменных и . В заключение параграфа выпишем нормированные волновые функции для ряда квантовых состояний водородоподобных атомов:

				Состояние
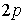
		+ 1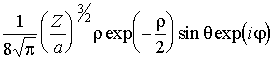
		- 1

На рис. 5.7 для некоторых квантовых состояний атома водорода, описываемых найденными волновыми функциями, показана радиальная электронная плотность вероятности в виде "облака", густота которого в разных точках пространства пропорциональна этой плотности вероятности. Именно так, в виде облака плотности вероятности может быть представлен образ атома в квантовой теории.

Поиск по сайту: