 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Інтеграл від вектор-функції
Невизначеним інтегралом від неперервної вектор-функції 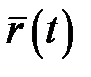 називається вектор-функція називається вектор-функція  така, що така, що  . .
|
Ця функція визначається з точністю до сталого векторного доданка.
Визначеним інтегралом від неперервної вектор-функції 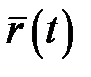 на відрізку на відрізку  називається сталий вектор, що знаходиться за формулою Ньютона-Лейбніца: називається сталий вектор, що знаходиться за формулою Ньютона-Лейбніца:  . .
|
Основні властивості інтегралів зберігаються і для векторних функцій, а саме:
1°. 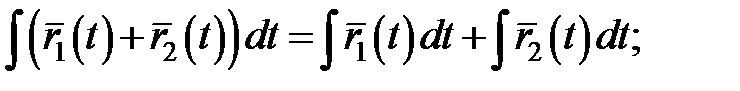
2°.  ;
;
3°.  якщо
якщо 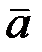 – сталий вектор;
– сталий вектор;
4°.  якщо
якщо 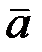 – сталий вектор;
– сталий вектор;
5°.  ;
;
6°. 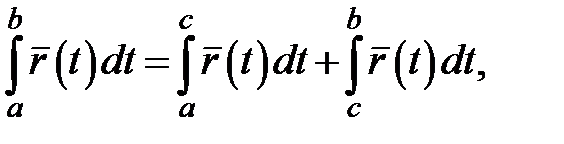 якщо функція
якщо функція  неперервна на відрізку
неперервна на відрізку  і
і  ;
;
7°.  .
.
Поиск по сайту: