 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Супровідний тригранник кривої
Оскільки при вивченні кривих використовують їх рівняння, то вибір системи координат впливає на вид рівняння. Наприклад, якщо центр еліпса вибрати за початок системи координат на площині еліпса, а координатні вісі сумістити з осями симетрії еліпса, то в такій системі координат еліпс визначається канонічним рівнянням. За канонічним рівнянням еліпса легко визначиться його розміри, фокуси, директриси.
Існує просторова система координат, яка пов’язана з кривою та її геометричними властивостями і яка зручна для побудови її локальної диференціальної геометрії.
Гладка крива  у кожній своїй точці
у кожній своїй точці 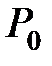 має єдину дотичну. Якщо
має єдину дотичну. Якщо  є годографом векторної функції
є годографом векторної функції  , то напрямним вектором дотичної є вектор
, то напрямним вектором дотичної є вектор  .
.
Якщо  – двічі неперервно диференційовна крива, то за умови
– двічі неперервно диференційовна крива, то за умови  у кожній своїй точці
у кожній своїй точці 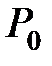 вона має єдину стичну площину, яка визначається точкою
вона має єдину стичну площину, яка визначається точкою 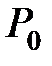 і векторами
і векторами  і
і  . За означенням стична площина кривої у точці
. За означенням стична площина кривої у точці 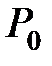 містить дотичну, проведену до кривої у точці
містить дотичну, проведену до кривої у точці 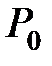 .
.
Нормаллю просторової кривої називається будь-яка пряма, яка перпендикулярна до дотичної і проходить через точку дотику. Таким чином, у будь-якій своїй точці гладка крива має нескінченну множину нормалей. Всі вони розміщені в одній площині, перпендикулярній до дотичної прямої – нормальній площині кривої.
Серед нормалей виділяють дві:
1) головну нормаль  , яка розміщена в стичній площині;
, яка розміщена в стичній площині;
2) бінормаль  , яка перпендикулярна до стичної площини.
, яка перпендикулярна до стичної площини.
| π3 |
| π2 |
| π1 |

|

|

|

|

|

|

|

|
| Рис.13 |
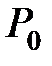 (рис. 13). Гранями супровідного тригранника є три взаємно перпендикулярні площини:
(рис. 13). Гранями супровідного тригранника є три взаємно перпендикулярні площини:
 – стична площина, яка містить дотичну
– стична площина, яка містить дотичну  і головну нормаль
і головну нормаль  ;
;
 – нормальна площина, яка містить головну нормаль
– нормальна площина, яка містить головну нормаль  і бінормаль
і бінормаль  ;
;
 – спрямна площина, яка містить бінормаль
– спрямна площина, яка містить бінормаль  і дотичну
і дотичну  .
.
Напрям ребер супровідного тригранника визначається векторами  ,
,  ,
,  . Часто зручно користуватися їх одиничними векторами
. Часто зручно користуватися їх одиничними векторами  відповідно, причому
відповідно, причому  ; трійка
; трійка  – права.
– права.
Якщо стична площина єдина, то супровідний тригранник у будь-якій  однозначно визначається точкою
однозначно визначається точкою 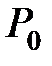 і ортонормованим базисом векторів
і ортонормованим базисом векторів  .
.
Якщо точка 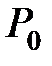 описує криву
описує криву  , то супровідний тригранник, рухаючись, змінює своє положення в просторі.
, то супровідний тригранник, рухаючись, змінює своє положення в просторі.
Система координат, напрям осей якої визначається векторами  називається природною. Вона широко використовується в механіці. З трьох площин супровідного тригранника найважливіше значення для кривої має стична площина.
називається природною. Вона широко використовується в механіці. З трьох площин супровідного тригранника найважливіше значення для кривої має стична площина.
Для складання рівнянь елементів супровідного тригранника треба вміти обчислювати напрямні вектори його ребер:  ,
,  ,
,  .
.
З рис.13 випливає, що  ,
,  .
.
Тому послідовність дій може бути такою:
1) знайти 
2) знайти 
3) знайти  або
або 
Контрольні питання до теми 3
1. Дайте означення дотичної до кривої в даній точці кривої.
2. Сформулюйте та доведіть теорему про існування та єдиність дотичної до кривої.
3. Запишіть рівняння дотичної для різних способів аналітичного задання просторової кривої.
4. Дайте означення нормалі до кривої в даній точці кривої.
5. Дайте означення нормальної площини до просторової кривої в даній точці кривої.
6. Запишіть рівняння нормальної площини для різних способів задання просторової кривої.
7. Запишіть рівняння дотичної та нормалі для різних способів аналітичного задання плоскої кривої. Поясніть спосіб їх отримання та зв'язок між ними.
8. Дайте означення стичної площини кривої в даній точці кривої.
9. Сформулюйте та доведіть теорему про існування стичної площини регулярної кривої. Запишіть рівняння стичної площини.
10. Яка площина є стичною, якщо крива плоска?
11. Наведіть властивості стичної площини.
12. Поясніть будову супровідного тригранника кривої: що є його ребрами і гранями.
13. Як знайти напрямні вектори ребер супровідного тригранника?
14. Як знайти нормальні вектори граней супровідного тригранника?
Тема 4. Поняття теорії кривих,
Поиск по сайту: