Список використаної та рекомендованої літератури

1. Александров А.Д., Нецветаев Н.Ю. Геометрия: Учебное пособие. – М.: Наука, 1990. – 672 с.

2. Аминов Ю.А. Дифференциальная геометрия и топология кривых. – М.: Наука, 1987. – 159 с.

3. Борисенко О.А. Диференціальна геометрія і топологія. – Х.: Основа, 1995. – 304 с.

4. Борисенко О.А., Ушакова Л.М. Аналітична геометрія. Х.: Основа,1993. – 192с.

5. Городецький В.В., Мартинюк О.В. Диференціальна геометрія в теоремах і задачах: Навчальний посібник – Чернівці: Рута, 2006. – 400 с.

6. Дифференциальная геометрия, топология, тензорный анализ. Сборник задач. Н.И. Кованцов, Г.М. Зражевская, В.Г. Кочаровсий, В.И. Михайловский – К.: – Вища школа, 1989. – 398 с.

7. Зоря В.Д., Рева Н.А. Еволюція поняття кривої // Науково-дослідна робота студентів як чинник удосконалення професійної підготовки майбутнього вчителя: зб. наук. пр./редкол.: Л.І.Білоусова та ін. – Х.: Факт, 2010 – Вип.2. – С. 77-84.

8. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: Учебник для вузов. – СПб.: Издательство «Лань», 2003. – 416 с.

9. Моденов П.С. Сборник задач по дифференциальной геометрии. – М.: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1949. – 239 с.

10. Норден А.П. Краткий курс дифференциальной геометрии. – М.: ГИФМЛ, 1958. – 244 с.

11. Погорелов А.В. Геометрия. — М.: Наука, 1983. – 288 с.

12. Погорелов А.В. Дифференциальная геометрия. – М.: Наука, 1969. – 176 с.

13. Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия: Первое знакомство. – М.: Едиториал УРСС, 2003. – 408 с.

14. Проскурня І.П., Проскурня О.І., Процай В.Ф. Математичні парадокси – джерело математичних відкриттів // Науково-дослідна робота студентів як чинник удосконалення професійної підготовки майбутнього вчителя: зб. наук. пр./редкол.: Л.І.Білоусова та ін. – Х.: Факт, 2010 – Вип.2. – С. 173-181.

15. Сборник задач по дифференциальной геометрии / Под. ред. А.С. Феденко. – М.: Наука, 1979. – 272 с.

16. Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч. 5. Тести. – Харків: ХНУРЕ, 2007. – 512 с.

ДОДАТОК 1

Питання для підготовки до вхідного контролю з навчальної дисципліни «Диференціальна геометрія та топологія»

Елементи лінійної алгебри

1. Що називається визначником другого порядку?

2. Що називається визначником третього порядку?

3. Сформулюйте основні властивості визначників.

4. Що називається мінором; алгебраїчним доповненням?

5. Запишіть розклад визначника за елементами першого рядка.

6. Як обчислюються визначники вищих порядків?

7. Що називається матрицею?

8. Що називається рангом матриці?

9. Як обчислити ранг матриці?

10. Яка система лінійних рівнянь називається однорідною? За якої умови однорідна система лінійних рівнянь має ненульові розв’язки?

11. Запишіть формули, які виражають ненульові розв’язки однорідної системи двох рівнянь з трьома невідомими через коефіцієнти системи.

Елементи векторної алгебри

1. Що називається геометричним вектором?

2. Які вектори називаються колінарними; компланарними?

3. Поясніть побудову суми двох векторів за правилом трикутника; за правилом паралелограма.

4. Дайте означення добутку вектора на число.

5. Дайте означення базису на площині; в просторі.

6. Запишіть розклад вектора за базисом на площині; в просторі.

7. Як знайти координати суми двох векторів; добутку вектора на число?

8. Що називається скалярним добутком двох векторів?

9. Сформулюйте алгебраїчні та геометричні властивості скалярного добутку.

10. Як знайти довжину вектора; кут між двома векторами; проекцію одного вектора на інший?

11. Що називається векторним добутком двох векторів?

12. Сформулюйте алгебраїчні та геометричні властивості векторного добутку.

13. Поясніть геометричний зміст модуля векторного добутку.

14. Що називається мішаним добутком трьох векторів?

15. Сформулюйте алгебраїчні та геометричні властивості мішаного добутку.

16. Поясніть геометричний зміст модуля мішаного добутку.

17. Запишіть формулу, за якою за координатами даних векторів у декартовій системі координат обчислюється їх скалярний добуток; векторний добуток; мішаний добуток?

18. Сформулюйте необхідну і достатню умову ортогональності двох векторів; колінеарності двох векторів; компланарності трьох векторів.

Елементи аналітичної геометрії

1. Запишіть загальне рівняння прямої на площині та поясніть геометричний зміст коефіцієнтів при змінних.

2. Поясніть геометричний зміст коефіцієнтів при змінних в загальному рівнянні площини.

3. Запишіть рівняння прямої на площині, яка проходить через дану точку перпендикулярно до даного вектора .

4. Запишіть рівняння прямої на площині, яка проходить через дану точку паралельно до даного вектора . Як називається це рівняння?

5. Запишіть рівняння прямої з кутовим коефіцієнтом та поясніть геометричний зміст параметрів, які в нього входять.

6. Запишіть рівняння прямої, якщо дано її кутовий коефіцієнт k і точка , через яку вона проходить.

7. Запишіть рівняння прямої на площині, яка проходить через дві дані точки , .

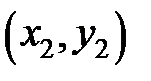8. Запишіть умови паралельності та перпендикулярності двох прямих на площині, заданих загальними рівняннями; канонічними рівняннями; рівняннями з кутовим коефіцієнтом.

9. Запишіть загальне рівняння площини та поясніть геометричний зміст коефіцієнтів при змінних.

10. Запишіть рівняння площини, яка проходить через дану точку перпендикулярно до даного вектора .

11. Запишіть рівняння площини, яка проходить через три дані точки , , .

12. Запишіть умови паралельності та перпендикулярності двох площин, заданих загальними рівняннями.

13. Запишіть канонічні рівняння прямої в просторі та поясніть геометричний зміст параметрів, які в нього входять.

14. Запишіть параметричні рівняння прямої в просторі та поясніть геометричний зміст коефіцієнтів, які в нього входять.

15. Запишіть рівняння прямої в просторі, яка проходить через дві дані точки , .

16. Запишіть загальне рівняння прямої в просторі та поясніть, як у цьому випадку знайти яку-небудь точку прямої та напрямний вектор.

17. Запишіть умови паралельності та перпендикулярності двох прямих в просторі, заданих канонічними рівняннями.

18. Запишіть умови паралельності та перпендикулярності прямої в просторі, заданої канонічним рівнянням 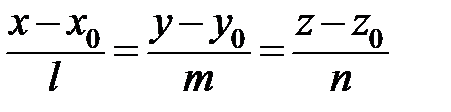, та площини .

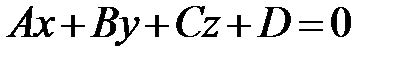Елементи математичного аналізу

1. Дайте означення функції.

2. Дайте означення границі функції. Сформулюйте та доведіть теореми про границі.

3. Дайте означення нескінченно малої функції, перелічіть властивості нескінченно малих функцій.

4. Дайте означення функції, неперервної в точці; неперервної на відрізку.

5. Наведіть властивості функцій, неперервних на відрізку.

6. Дайте означення похідної функції. Поясніть її геометричний та механічний зміст.

7. Сформулюйте та доведіть теореми про похідні суми, добутку та частки двох функцій.

8. Виведіть формули похідних основних елементарних функцій.

9. Як знаходиться похідна від складеної функції?

10. Дайте означення похідної n –го порядку.

11. Запишіть формулу Тейлора.

12. Дайте означення невизначеного інтеграла.

13. Запишіть формулу Ньютона-Лейбніца обчислення визначеного інтеграла.

Поиск по сайту: