 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі
| Умова | Варіанти відповідей | |
| 1. | Вказати походження означення плоскої кривої:
1) множина точок на площині, координати яких задовольняють рівнянню  ;
2) траєкторія рухомої точки з координатами, які залежать від часу;
3) досконала, зв’язна множина точок площини, жодна з точок якої не є внутрішньою;
4) множина точок, координати яких є неперервними функціями від деякого параметра t, який змінюється на відрізку  числової осі;
5) довільний континуум розмірністю одиниця.
| а) з механіки; б) за Жорданом; в) за Декартом; г) за Урисоном; д) за Кантором. |
| 2. | Яка лінія є класичним прикладом неможливості застосування до дослідження її властивостей визначення лінії, яке дав Декарт? | а) крива Пеано; б) килим Серпінського. в) спіраль Архімеда; г) відсутня у даному списку; д) будь-яка із а,б,в. |
| 3. | Навести класичний приклад кривої, яка не задовольняє означенню кривої: 1) за Жорданом; 2) за Кантором. | а) крива Пеано; б) килим Серпінського. в) спіраль Архімеда; г) відсутня у даному списку; д) будь-яка із а,б,в. |
| 4. | Як називається неперервне відображення, при якому образом відрізка  є цілий квадрат на площині?
| а) крива Пеано; б) килим Серпінського. в) спіраль Архімеда; г) відсутня у даному списку; д) будь-яка із а,б,в. |
| 5. | Яка із вказаних кривих задовольняє канторовому означенню кривої, але не відповідає наочним уявленням про лінію? | а) крива Пеано; б) килим Серпінського. в) спіраль Архімеда; г) відсутня у даному списку; д) будь-яка із а,б,в. |
| 6. | Нехай  :  . Яке твердження справджується, якщо:
1) φ – відображення;
2) φ – неперервне відображення;
3) φ – взаємно однозначне відображення;
4)  – відображення, обернене до φ.
| а) близькі точки з  відображаються в близькі точки з  ;
б) в кожну точку відображається тількиодна точка з ;
в) кожній точці з відповідає тількиодна точка з ;
г) кожній точці з відповідає тількиодна точка з ;
д) якщо Х   і  , то  .
|
| 7. | Яким умовам має задовольняти відображення φ, якщо воно є топологічним? | а) φ – однозначне відображення;
б) φ – взаємно однозначне відображення;
в) φ – неперервне відображення;
г) – взаємно однозначне відображення;
д) – неперервне відображення.
|
| 8. | Як називається крива, яка є: 1) образом інтервалу при його топологічному відображенні в простір або на площину; 2) топологічним образом або відкритого відрізка прямої, або кола; 3) топологічним образом кола; 4) образом простої кривої при її локально топологічному відображенні в простір? | а) елементарна крива; б) проста крива; в) замкнена крива; г) регулярна крива; д) загальна крива. |
| 9. | Який вид має: 1) параметричне рівняння кривої у векторній формі; 2) параметричні рівняння просторової кривої в скалярній формі; 3) параметричне рівняння плоскої кривої; 4) рівняння неявно заданої просторової кривої; 5) рівняння неявно заданої плоскої кривої; 6) рівняння явно заданої плоскої кривої. | а)  ;
б) 
в) 
г) 
д) 
е) 
|
| 10. | За яких умов рівняння визначатимуть регулярну просторову криву в околі її точки  , якщо криву задано:
1) параметричним рівнянням у векторній формі;
2) параметричним рівнянням в скалярній формі;
3) кривої, заданої неявно.
| а) ранг матриці 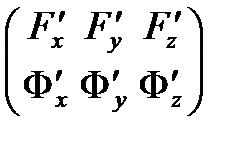 дорівнює 2;
б)  ;
в)  .
г) функції  неперервні разом зі своїми частинними похідними в околі ;
д) функція 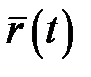 має неперервну похідну в околі ;
е) функції  ,  ,  мають неперервні похідні в околі .
|
| 11. | За яких умов рівняння визначатимуть регулярну плоску криву в околі її точки  , якщо криву задано:
1) параметричним рівнянням в скалярній формі;
2) явно;
3) неявно.
| а)  ;
б)  ;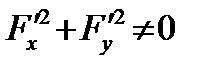
в) функція  неперервна разом зі своїми частинними похідними в околі ;
г) функції , мають неперервні похідні в околі ;
д) функції  і  неперервні в околі ;
е)  .
|
Поиск по сайту: