АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Випадок плоскої кривої

Читайте также:
  1. Дискретний випадок
  2. Добові норми продовольства, яке закладається на пункти управління та сховища на випадок виникнення НС у перерахунку на одну людину на добу
  3. Довжина дуги кривої. Натуральна параметризація
  4. Дотична пряма просторової кривої
  5. Збори до Фонду страхування на випадок безробіття
  6. Методика побудови опорної кривої
  7. Неперервний випадок
  8. Нормальна площина просторової кривої
  9. Поняття кривої
  10. Поняття площі плоскої фігури, її основні властивості та способи вимірювання. Рівновеликі та рівноскладені фігури. Одиниці вимірювання площі та співвідношення між ними.
  11. Прямої, ламаної та кривої ліній.

Вважатимемо, що всі точки кривої γ належать деякій площині, наприклад, Оху, для якої . Тоді маємо такі способи аналітичного задання плоскої кривої.

а) Параметричні рівняння плоскої кривої в скалярній формі:

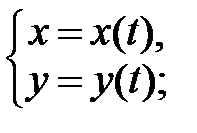(1´)

б) Параметричне рівняння у векторній формі:

; (2´)

в) Явно задана плоска крива :

(3´)

г) Неявно задана плоска крива:

(4´)

Рівняння (4´) визначають регулярну елементарну криву в деякому околі її точки , якщо функція неперервна разом зі своїми частинними похідними в околі цієї точки і в цій точці .

 

Контрольні питання до теми 2

1. Дайте означення топологічного відображення. Поясніть зміст понять, які вживаються в цьому означенні.

2. Дайте означення елементарної кривої; регулярної кривої, гладкої, загальної кривої. Наведіть приклади.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)